Репетиторы
Законы кеплера и движение планет
[Latexpage]
"планета" происходит от греческого слова, означающего "странник", и действительно планеты постоянно меняют свое положение в небе относительно звезд. Одним из самых великих интеллектуальных достижений 16-го и 17-го веков было осознание того, что Земля это тоже планета, все планеты вращаются вокруг Солнца, и движения планет, наблюдаемое с Земли, может быть использовано для весьма точного определения их орбит.
Первая и вторая из этих идей были опубликованы Николаем Коперником в Польше в 1543 году. Законы, по которым движутся планеты, были выведены между 1601 и 1619 годами немецким астрономом и математиком Йоханнесом Кеплером. Он использовал громадное (по меркам того столетия) количество точных данных о видимых планетарных движениях, собранных его наставником, датский астрономом Тихо Браге. Методом проб и ошибок Кеплер обнаружил три эмпирических закона, которые точно описывали движения планеты:
Каждая планета солнечной системы движется по эллиптической орбите с солнцем...
Читать далее
Читать далее
Искусственные спутники Земли
[Latexpage]
�твенные спутники, вращающиеся вокруг Земли - всем известная современная технология.(Рис. 1). Но возникает вопрос: как они остаются на орбите, и как определяются их орбиты? Мы используем законы Ньютона и закон гравитации, чтобы найти ответы. К тому же движение планет можно анализировать таким же образом.
Рисунок 1. Космический телескоп Хабл один из крупнейших спутников выведеных на орбиту весит 11 тонн и имеет длину 13,5 м.Для начала представим себе мотоциклиста, который, разогнавшись по горизонтальной поверхности, прыгает с обрыва. Если он выживет и повторит эксперимент с увеличенной скоростью разгона, он приземлится дальше, чем в первый раз. Мы можем представить его разогнавшимся до достаточно большой скорости, чтобы искривление Земли стало значительным. Тоесть он будет падать,а земля будет изгибаться под ним. Если он будет ехать достаточно быстро, и если его точка "запуска" будет достаточно высоко, чтобы не касаться вершин гор, он сможет летать вокруг Земли не при...
Читать далее
Читать далее
КПД механизма
[Latexpage]
ктике приходится различать полезную работу Aполезн, которую нужно совершить при помощи механизма в идеальных условиях отсутствия каких-либо потерь, и полную работу Aполн, которая совершается для тех же целей в реальной ситуации.
Полная работа равна сумме:
полезной работы;
работы, совершённой против сил трения в различных частях механизма;
работы, совершённой по перемещению составных элементов механизма.
Так, при подъёме груза рычагом приходится вдобавок совершать работу по преодолению силы трения в оси рычага и по перемещению самого рычага, имеющего некоторый вес.
Полная работа всегда больше полезной. Отношение полезной работы к полной называется
коэффициентом полезного действия (КПД) механизма:
η = Aполезн/Aполн.КПД принято выражать в процентах. КПД реальных механизмов всегда меньше 100%. Вычислим КПД наклонной плоскости с углом $\alpha$ при наличии трения. Коэффициент трения между поверхностью наклонной плоскости и грузом равен $\mu$.
Найди...
Читать далее
Читать далее
Простые механизмы
[Latexpage]
�змом в физике называется приспособление для преобразования силы (её увеличения или уменьшения). Например, прикладывая небольшое усилие в одном месте механизма, можно получить значительно большее усилие в другом его месте. Один вид механизма нам уже встретился: это гидравлический пресс. Здесь мы рассмотрим так называемые простые механизмы — рычаг и наклонную плоскость.
Рычаг
Рычаг — это твёрдое тело, которое может вращаться вокруг неподвижной оси. На рис. 1 изображён рычаг с осью вращения O. К концам рычага (точкам A и B) приложены силы $\vec{F}_1$ и $\vec{F}_2$. Плечи этих сил равны соответственно $l_1$ и $l_2$.
Рис. 1. Рычаг
Условие равновесия рычага даётся правилом моментов: $F_1 l_1 = F_2 l_2$, откуда
$$ \frac{F_1}{F_2} = \frac { l_2 }{ l_1 }. $$
Из этого соотношения следует, что рычаг даёт выигрыш в силе или в расстоянии (смотря по тому, с какой целью он используется) во столько раз, во сколько большее плечо длиннее меньшего.
Например, чтобы усилием...
Читать далее
Читать далее
Закон сохранения механической энергии
[Latexpage]
�вативные силы называются так потому, что сохраняют механическую энергию замкнутой системы тел. Механическая энергия $E$ тела равна сумме его кинетической и потенциальной энергий:
$$E = K + W.$$
Механическая энергия системы тел равна сумме их кинетических энергий и потенциальной энергии их взаимодействия друг с другом.
Предположим, что тело совершает движение под действием силы тяжести и/или силы упругости пружины. Будем считать, что трения нет. Пусть в начальном положении кинетическая и потенциальная энергии тела равны $K_1$ и $W_1$, в конечном положении — $K_2$ и $W_2$. Работу внешних сил при перемещении тела из начального положения в конечное обозначим $A$.
По теореме о кинетической энергии:
$$K_2 - K_1 = A.$$
Но работа консервативных сил равна разности потенциальных энергий:
$$A = W_1 - W_2.$$
Отсюда получаем:
$$K_2 - K_1 = W_1 - W_2,$$
или
$$K_1 + W_1 = K_2 + W_2.$$
Левая и правая части данного равенства представляют собой механическую энергию тела в начал...
Читать далее
Читать далее
Потенциальная энергия
[Latexpage]
="font-size: large;">Потенциальная энергия тела вблизи поверхности Земли
Рассмотрим тело массы $m$, находящееся на некоторой высоте над поверхностью Земли. Высоту считаем много меньше земного радиуса. Изменением силы тяжести в процессе перемещения тела пренебрегаем.
Если тело находится на высоте $h$, то потенциальная энергия тела по определению равна:
$$ W = m g h,$$
где $g$ — ускорение свободного падения вблизи поверхности Земли. Высоту не обязательно отсчитывать от поверхности
Земли. Как мы увидим ниже (формулы (\ref{W1}), (\ref{W2})), физическим смыслом обладает не сама по себе потенциальная энергия, но её изменение. А изменение потенциальной энергии не зависит от уровня отсчёта. Выбор нулевого уровня потенциальной энергии в конкретной задаче диктуется исключительно соображениями удобства.
Найди репетитора по физики
Выбери преподавателя для подготовки к экзаменам и контрольным работам
Искать репетитора
Найдём работу, совершаемую силой тяжест...
Читать далее
Читать далее
Кинетическая энергия
[Latexpage]
�я является мерой движения и взаимодействия любых объектов в природе. Имеются различные формы энергии: механическая, тепловая, электромагнитная, ядерная. . .
Опыт показывает, что энергия не появляется ниоткуда и не исчезает бесследно, она лишь переходит из одной формы в другую. Это самая общая формулировка закона сохранения энергии.
Каждый вид энергии представляет собой некоторое математическое выражение. Закон сохранения энергии означает, что в каждом явлении природы определённая сумма таких выражений остаётся постоянной с течением времени.
Измеряется энергия в джоулях, как и работа. Механическая энергия является мерой движения и взаимодействия механических объектов(материальных точек, твёрдых тел).
Мерой движения тела является кинетическая энергия. Она зависит от скорости тела. Мерой взаимодействия тел является потенциальная энергия. Она зависит от взаимного расположениятел.
Механическая энергия системы тел равна сумме кинетической энергии тел и потенциальной ...
Читать далее
Читать далее
Работа. Мощность
[Latexpage]
an style="font-size: large;">Работа
Пусть на тело действует постоянная сила $\vec{F}$ и тело, двигаясь прямолинейно по горизонтальной поверхности, совершило перемещение $\vec{s}$. Сила $\vec{F}$ не обязательно является непосредственной причиной перемещения (так, сила тяжести не является непосредственной причиной перемещения шкафа, который передвигают по комнате).
Предположим сначала, что векторы силы и перемещения сонаправлены (рис. 1; остальные силы, действующие на тело, не указаны).
В этом простейшем случае работа $A$ определяется как произведение модуля силы на модуль
перемещения:
\begin{equation}\label{A1}
A = F s.
\end{equation}
Единицей измерения работы служит джоуль (Дж): Дж = Н · м. Таким образом, если под действием силы 1 Н тело перемещается на 1 м, то сила совершает работу 1 Дж.
Работа силы, перпендикулярной перемещению, по определению считается равной нулю. Так, в данном случае сила тяжести и сила реакции опоры не совершают работы.
Пусть тепе...
Читать далее
Читать далее
Закон сохранения импульса
[Latexpage]
="font-size: large;">Импульс системы тел
Начнём с простой ситуации системы двух тел. А именно, пусть имеются тело 1 и тело 2 с импульсами $\vec{p_1}$ и $\vec{p_2}$ соответственно. Импульс $\vec{p}$ системы данных тел — это векторная сумма импульсов каждого тела:
$$ \vec{p} = \vec{p_1} + \vec{p_2}.$$
Оказывается, для импульса системы тел имеется формула, аналогичная второму закону Ньютона в виде $\frac{d \vec{p} }{ d t } = \vec{F} .$ Давайте выведем эту формулу.
Все остальные объекты, с которыми взаимодействуют рассматриваемые нами тела 1 и 2, мы будем называть внешними телами. Силы, с которыми внешние тела действуют на тела 1 и 2, называем внешними силами. Пусть $\vec{F}_1$ — результирующая внешняя сила, действующая на тело 1. Аналогично $\vec{F}_2$ — результирующая внешняя сила, действующая на тело 2 (рис. 1).
Рисунок 1. Система двух телКроме того, тела 1 и 2 могут взаимодействовать друг с другом. Пусть тело 2 действует на тело 1 с силой $\vec{T}$. Тогда тело...
Читать далее
Читать далее
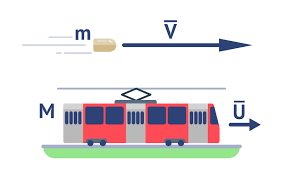
Импульс тела
[Latexpage]
>Импульс тела — это векторная величина, равная произведению массы тела на его скорость:
$$\vec{p} = m\vec{v}.$$
Специальных единиц измерения импульса нет. Размерность импульса — это просто произведение размерности массы на размерность скорости:
$[p] = [m] · [v] = $ (кг·м)/с.Почему понятие импульса является интересным? Оказывается, с его помощью можно придать второму закону Ньютона несколько иную, также чрезвычайно полезную форму.
Второй закон Ньютона в импульсной форме
Пусть $\vec{F}$ — равнодействующая сил, приложенных к телу массы $m$. Начинаем с обычной записи второго закона Ньютона:
$$m\vec{a} = \vec{F} . $$
С учётом того, что ускорение тела $\vec{a}$ равно производной вектора скорости, второй закон Ньютона переписывается следующим образом:
$$ m \frac{d\vec{v}}{dt} = \vec{F} . $$
Вносим константу $ m $ под знак производной:
$$ \frac{d m \vec{v}}{dt} = \vec{F} . $$
Как видим, в левой части получилась производная импульса:
\begin{equation} \label{p}
\f...
Читать далее
Читать далее