Потенциальная энергия

Главная

›

Материалы ›

Физика ›

Механическое движение. Механика ›

Потенциальная энергия

›

Выбирай среди 25000+ репетиторов из больше 100 предметов

Найти репетитора

Потенциальная энергия тела вблизи поверхности Земли

Рассмотрим тело массы $m$ , находящееся на некоторой высоте над поверхностью Земли. Высоту считаем много меньше земного радиуса. Изменением силы тяжести в процессе перемещения тела пренебрегаем.

Если тело находится на высоте $h$ , то потенциальная энергия тела по определению равна:

$W = m g h,$

где $g$ — ускорение свободного падения вблизи поверхности Земли. Высоту не обязательно отсчитывать от поверхности
Земли. Как мы увидим ниже (формулы (1), (2)), физическим смыслом обладает не сама по себе потенциальная энергия, но её изменение. А изменение потенциальной энергии не зависит от уровня отсчёта. Выбор нулевого уровня потенциальной энергии в конкретной задаче диктуется исключительно соображениями удобства.

Найди репетитора по физики

Выбери преподавателя для подготовки к экзаменам и контрольным работам

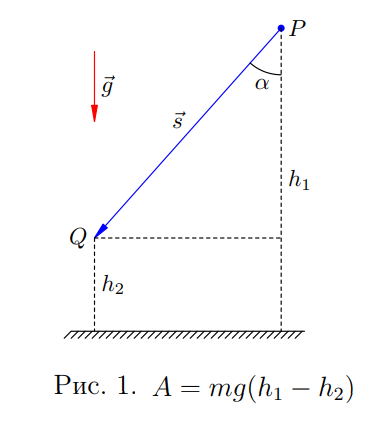
Найдём работу, совершаемую силой тяжести при перемещении тела. Предположим, что тело
перемещается по прямой из точки P, находящейся на высоте $h_1$ , в точку Q, находящуюся на высоте $h_2$ (рис. 1).

Угол между силой тяжести $m\vec{g}$ и перемещением тела $\vec{s}$ обозначим $\alpha$ . Для работы силы тяжести получим:

$A = m\vec{g} \vec{s} = m g s cos \alpha.$

Но, как видно из рис. 1, $s cos \alpha = h_1 - h_2$ . Поэтому

$A = m g (h_1 − h_2) = m g h_1 - m g h_2,$

или

(1) $\begin{equation*} A = W_1 - W_2. \end{equation*}$

Учитывая, что $W_1 - W_2 = -(W_2 - W_1) = - \Delta W$ , имеем также:

(2) $\begin{equation*} A = - \Delta W. \end{equation*}$

Можно доказать, что формулы (1) и (2) справедливы для любой траектории, по которой тело перемещается из точки P в точку Q, а не только для прямолинейного отрезка.

Работа силы тяжести не зависит от формы траектории, по которой перемещается тело, и равна разности значений потенциальной энергии в начальной и конечной точках траектории. Иными словами, работа силы тяжести всегда равна изменению потенциальной энергии с противоположным знаком. В частности, работа силы тяжести по любому замкнутому пути равна нулю.
Сила называется консервативной, если при перемещении тела работа этой силы не зависит
от формы траектории, а определяется только начальным и конечным положением тела. Сила тяжести, таким образом, является консервативной. Работа консервативной силы по любому замкнутому пути равна нулю. Только в случае консервативной силы возможно ввести такую величину, как потенциальная энергия.

Потенциальная энергия деформированной пружины

Рассмотрим пружину жёсткости $k$ . Начальная деформация пружины равна $x_1$ . Предположим, что пружина деформируется до некоторой конечной величины деформации $x_2$ . Чему равна при этом работа силы упругости пружины?
В данном случае силу на перемещение не умножишь, так как сила упругости меняется в процессе деформации пружины. Для нахождения работы переменной силы требуется интегрирование. Мы не будем приводить здесь вывод, а сразу выпишем конечный результат.

Оказывается, сила упругости пружины также является консервативной. Её работа зависит лишь от величин $x_1$ , $x_2$ и определяется формулой:

$A = \frac{kx^2_1}{2} - \frac{kx^2_2}{2}.$

Величина

$W = \frac{kx^2}{2}$

называется потенциальной энергией деформированной пружины ( $x$ — величина деформации). Следовательно,

$A = W_1 - W_2 = - \Delta W,$

что полностью аналогично формулам (1) и (2).