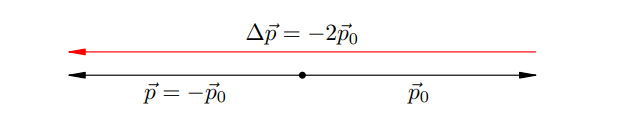Импульс тела
Импульс тела — это векторная величина, равная произведению массы тела на его скорость:
![]()
Специальных единиц измерения импульса нет. Размерность импульса — это просто произведение размерности массы на размерность скорости:
Второй закон Ньютона в импульсной форме
Пусть ![]() — равнодействующая сил, приложенных к телу массы
— равнодействующая сил, приложенных к телу массы ![]() . Начинаем с обычной записи второго закона Ньютона:
. Начинаем с обычной записи второго закона Ньютона:
![]()
С учётом того, что ускорение тела ![]() равно производной вектора скорости, второй закон Ньютона переписывается следующим образом:
равно производной вектора скорости, второй закон Ньютона переписывается следующим образом:
![]()
Вносим константу ![]() под знак производной:
под знак производной:
![]()
Как видим, в левой части получилась производная импульса:
(1) ![]()
Соотношение (1) и есть новая форма записи второго закона Ньютона.
Второй закон Ньютона в импульсной форме. Производная импульса тела есть равнодействующая приложенных к телу сил.
Можно сказать и так: результирующая сила, действующая на тело, равна скорости изменения импульса тела. Производную в формуле (1) можно заменить на отношение конечных приращений:
(2) ![]()
В этом случае ![]() есть средняя сила, действующая на тело в течение интервала времени
есть средняя сила, действующая на тело в течение интервала времени ![]() . Чем
. Чем
меньше величина ![]() , тем ближе отношение
, тем ближе отношение ![]() к производной
к производной ![]() , и тем ближе средняя сила
, и тем ближе средняя сила ![]() к своему мгновенному значению в данный момент времени.
к своему мгновенному значению в данный момент времени.
В задачах, как правило, интервал времени ![]() достаточно мал. Например, это может быть время соударения мяча со стенкой, и тогда
достаточно мал. Например, это может быть время соударения мяча со стенкой, и тогда ![]() — средняя сила, действующая на мяч со стороны стенки во время удара.
— средняя сила, действующая на мяч со стороны стенки во время удара.

Вектор ![]() в левой части соотношения (2) называется изменением импульса за время
в левой части соотношения (2) называется изменением импульса за время ![]() . Изменение импульса — это разность конечного и начального векторов импульса. А именно, если
. Изменение импульса — это разность конечного и начального векторов импульса. А именно, если ![]() — импульс тела в некоторый начальный момент времени,
— импульс тела в некоторый начальный момент времени, ![]() — импульс тела спустя промежуток времени
— импульс тела спустя промежуток времени ![]() , то изменение импульса есть разность:
, то изменение импульса есть разность:
![]()
Подчеркнём ещё раз, что изменение импульса — это разность векторов. Напомним, что при построении разности векторов нужно совместить начала обоих векторов, соединить их концы и «уколоть» стрелкой тот вектор, из которого производится вычитание.
Пусть, например, мяч летит перпендикулярно стенке (импульс перед ударом равен ![]() ) и отскакивает назад без потери скорости (импульс после удара равен
) и отскакивает назад без потери скорости (импульс после удара равен ![]() ). Несмотря на то, что импульс по модулю не изменился
). Несмотря на то, что импульс по модулю не изменился ![]() , изменение импульса нулю не равно:
, изменение импульса нулю не равно:
![]()
Модуль изменения импульса, как видим, равен удвоенному модулю начального импульса мяча: ![]()
Перепишем формулу (2) следующим образом:
(3) ![]()
или, расписывая изменение импульса, как и выше:
![]()
Величина ![]() называется импульсом силы. Специальной единицы измерения для импульса силы нет; размерность импульса силы равна просто произведению размерностей силы и времени:
называется импульсом силы. Специальной единицы измерения для импульса силы нет; размерность импульса силы равна просто произведению размерностей силы и времени:
(Обратите внимание, что Н·с оказывается ещё одной возможной единицей измерения импульса тела.)
Словесная формулировка равенства (3) такова: изменение импульса тела равно импульсу действующей на тело силы за данный промежуток времени. Это, разумеется, снова есть второй закон Ньютона в импульсной форме.