Искусственные спутники Земли

Искусственные спутники, вращающиеся вокруг Земли — всем известная современная технология.(Рис. 1). Но возникает вопрос: как они остаются на орбите, и как определяются  их орбиты? Мы используем законы Ньютона и закон гравитации, чтобы найти ответы. К тому же движение планет можно анализировать таким же образом.

Рисунок 1. Космический телескоп Хабл один из крупнейших спутников выведеных на орбиту весит 11 тонн и имеет длину 13,5 м.Для начала представим себе мотоциклиста, который, разогнавшись по горизонтальной поверхности, прыгает с обрыва. Если он выживет и повторит эксперимент с увеличенной скоростью разгона, он приземлится дальше, чем в первый раз. Мы можем представить его разогнавшимся до достаточно большой скорости, чтобы искривление Земли стало значительным. Тоесть он будет падать,а земля будет изгибаться под ним. Если он будет ехать достаточно быстро, и если его точка «запуска» будет достаточно высоко, чтобы не касаться вершин гор, он сможет летать вокруг Земли не приземляясь.

На рисунке 2 показаны варианты этих «запусков». Мы запускаем снаряд из точки А вдоль прямой AB, касательное к поверхности земли. Траектории с 1 по 7 показывают как траектория меняется в зависимости от начальной скорости. На траекториях с 3 по 5 снаряд не падает на землю и становится спутником. Если нет замедляющей силы, то скорость снаряда, когда он возвращается в точку A, равна его начальной скорости и он повторяет свое движение до бесконечности.

Рисунок. 2. Траектории спутников в зависимости от начальной скорости
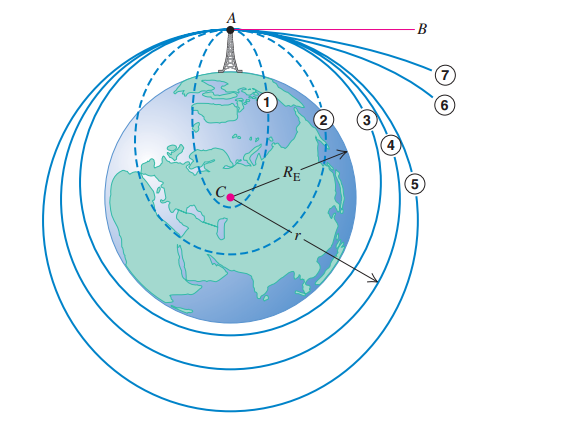
Траектории с 1 по 5 замыкаются и называются замкнутыми орбитами. Все замкнутые орбиты — это эллипсы или сегменты эллипсов; Траектория 4 представляет собой круг, особый случай эллипса. Траектории 6 и 7 являются открытыми орбитами. Для этих путей снаряд никогда не возвращается к его отправной точке и уходит все дальше от земли.

Спутники: круговые орбиты

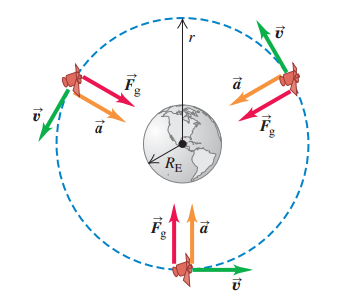
Круговая орбита, указанная на рис.2 как траектория 4, является простейшим случаем. Но в то же время очень важный, поскольку многие искусственные спутники имеют почти круговые орбиты, как и орбиты планет вокруг Солнца. Единственная сила, действующая на спутник на круговой орбите вокруг Земли является гравитационным притяжением Земли, которая направлена к центру земли и, следовательно, к центру орбиты-круга (рис. 3). Это означает, что спутник совершает равномерное круговое движение и его скорость постоянна. Спутник не падает на Землю; скорее он постоянно падает вокруг земли.

Рисунок. 3. Сила гравитации, которая действует на спутникНа круговой орбите скорость спутника как раз не должна меняться для поддержания расстояние постоянным от спутника до центра Земли. Давайте посмотрим, как найти постоянную скорость спутника на круговой орбите. Радиус орбиты , измеренный от центра Земли; Ускорение спутника имеет величину и всегда направлено на центр круга. Гравитационная сила, которая действует на спутник массы направлена в том же направлении, что и ускорение:

   

где — масса Земли.
Согласно второму закону Ньютона () имеем:

   

Отсюда

(1)  

Эта скорость в литературе называется первой космической скоростью.
В формуле (1) нет массы спутника, а это означает, что скорость спутника не зависит от его массы. Если бы мы могли разрезать спутник пополам, не меняя его скорости, каждая половина продолжала бы двигаться с той же скорость, что и целый спутник.

Астронавт на борту космической станции тоже является спутником Земли, который удерживается гравитационным притяжением Земли на той же орбите, что и станция. Астронавт имеет ту же скорость и ускорение, что и станция, поэтому никакая сила не толкает его к любой из стенок станции. Человек находится в состоянии кажущейся невесомости, как в свободно падающем лифте. (полная невесомость возникнет, только если космонавт будет бесконечно удален от любых других масс, так что гравитационная сила действующая на него будет равна нулю.) Действительно, каждая часть его тела почти невесома; он ничего не чувствует, прижимая живот к кишечнику или голову к плеч.

Кажущаяся невесомость — это не просто особенность круговых орбит; это происходит, когда гравитация является единственной силой, действующей на космический корабль. Следовательно, это происходит для орбит любой формы, включая открытые орбиты, такие как траектории 6 и 7 на рис. 2.

Мы можем вывести соотношение между радиусом круговой орбиты и периодом — временем одного оборота. Скорость — это расстояние, пройденное за один оборот, деленное на период:
\begin{eqution}\label{2}
v = \frac{2 \pi r}{T}
\end{equation}
Из (??) находим, чему будет равняться , подставив значение скорости из (1):
\begin{eqution}\label{3}
T = \frac{ 2 \pi r}{v} = 2 \pi r \sqrt{\frac{r}{GM}} = \frac{2 \pi r^{\frac{3}{2}}}{\sqrt{GM}}
\end{equation}
Уравнения (1) и (??) показывают, что большие орбиты соответствуют более медленным скоростям и более длительным периоды. В качестве примера, орбита Международной космической станции 6800 км от центра Земли (400 км над земной поверхностью) с орбитальная скорость 7,7 км/с и орбитальный периодом 93 минуты. Лунная орбита Земли на гораздо большей растоянии радиусом 384 000 км, и поэтому имеет гораздо более меньшую орбитальную скорость (1,0 км/с) и значительно более длинный орбитальный период (27,3 дня).

Поскольку скорость на круговой орбите для заданного радиуса орбиты определяется по формуле (1), то можно определить полную механическую энергия спутника.

   

Полная механическая энергия на круговой орбите отрицательна и равна половине потенциальной энергии. Увеличение радиуса орбиты означает увеличение механической энергии (то есть, полная энергия стает менее отрицательной). Если спутник находится на относительно низкой орбите, которая сталкивается с внешними границами земной атмосферы, механическая энергия уменьшается из-за негативной работы, проделанной силой сопротивления воздуха; в результате радиус орбиты уменьшается до тех пор, пока спутник не упадет на землю или не сгорит в атмосфере.
Мы говорили в основном о земных спутниках, но мы можем применить тот же самый анализ к круговому движению любого человека, находящегося под гравитационным притяжением к стационарному телу.