Работа. Мощность
Работа
Пусть на тело действует постоянная сила ![]() и тело, двигаясь прямолинейно по горизонтальной поверхности, совершило перемещение
и тело, двигаясь прямолинейно по горизонтальной поверхности, совершило перемещение ![]() . Сила
. Сила ![]() не обязательно является непосредственной причиной перемещения (так, сила тяжести не является непосредственной причиной перемещения шкафа, который передвигают по комнате).
не обязательно является непосредственной причиной перемещения (так, сила тяжести не является непосредственной причиной перемещения шкафа, который передвигают по комнате).
Предположим сначала, что векторы силы и перемещения сонаправлены (рис. 1; остальные силы, действующие на тело, не указаны).
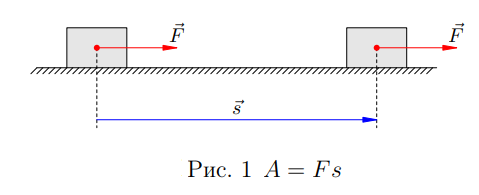
В этом простейшем случае работа ![]() определяется как произведение модуля силы на модуль
определяется как произведение модуля силы на модуль
перемещения:
(1) ![]()
Единицей измерения работы служит джоуль (Дж): Дж = Н · м. Таким образом, если под действием силы 1 Н тело перемещается на 1 м, то сила совершает работу 1 Дж.
Работа силы, перпендикулярной перемещению, по определению считается равной нулю. Так, в данном случае сила тяжести и сила реакции опоры не совершают работы.
Пусть теперь вектор силы образует с вектором перемещения острый угол ![]() (рис. 2).
(рис. 2).
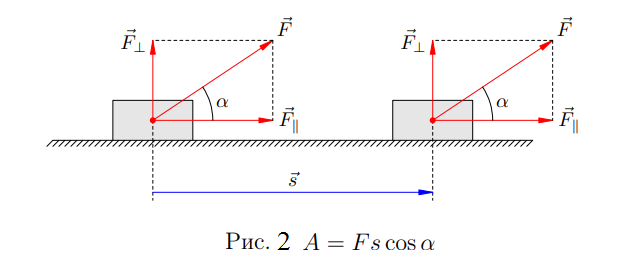
Разложим силу ![]() на две составляющие:
на две составляющие: ![]() (параллельную перемещению) и
(параллельную перемещению) и ![]() (перпендикулярную перемещению). Работу совершает только
(перпендикулярную перемещению). Работу совершает только ![]() . Поэтому для работы силы
. Поэтому для работы силы ![]() получаем:
получаем:
![]() Итак,
Итак,
(2) ![]()
Если вектор силы образует с вектором перемещения тупой угол ![]() , то работа по-прежнему определяется формулой (2). В этом случае работа оказывается отрицательной.
, то работа по-прежнему определяется формулой (2). В этом случае работа оказывается отрицательной.

Например, работа силы трения скольжения, действующей на тело в рассмотренных ситуациях, будет отрицательной, так как сила трения направлена противоположно перемещению. В этом случае имеем: ![]() = 180◦,
= 180◦, ![]() , и для работы силы трения получаем:
, и для работы силы трения получаем:
![]()
где ![]() — масса тела,
— масса тела, ![]() — коэффициент трения между телом и опорой.
— коэффициент трения между телом и опорой.
Соотношение (2) означает, что работа является скалярным произведением векторов силы и перемещения:
![]()
Это позволяет вычислять работу через координаты данных векторов:
![]()
Пусть на тело действуют несколько сил ![]() и
и ![]() — равнодействующая этих сил. Для работы силы
— равнодействующая этих сил. Для работы силы ![]() имеем:
имеем:
![]()
или
![]()
где ![]() — работы сил
— работы сил ![]()
Итак, работа равнодействующей приложенных к телу сил равна сумме работ каждой силы в отдельности.
Мощность
Часто имеет значение быстрота, с которой совершается работа. Скажем, на практике важно знать, какую работу сможет выполнить данное устройство за фиксированное время.
Мощность — это величина, характеризующая скорость совершения работы. Мощность ![]()
есть отношение работы ![]() ко времени
ко времени ![]() , за которое эта работа совершена:
, за которое эта работа совершена:
![]()
Мощность измеряется в ваттах (Вт). 1 Вт = 1 Дж/с, то есть 1 Вт — это такая мощность, при которой работа в 1 Дж совершается за 1 с.
Предположим, что силы, действующие на тело, уравновешены, и тело движется равномерно и прямолинейно со скоростью ![]() . В этом случае существует полезная формула для мощности, развиваемой одной из действующих сил
. В этом случае существует полезная формула для мощности, развиваемой одной из действующих сил ![]() .
.
За время ![]() тело совершит перемещение
тело совершит перемещение ![]() Работа силы
Работа силы ![]() будет равна:
будет равна:
![]()
Отсюда получаем мощность:
![]()
или
![]()
где ![]() — угол между векторами силы и скорости.
— угол между векторами силы и скорости.
Наиболее часто эта формула используется в ситуации, когда ![]() — «сила тяги» двигателя автомобиля (которая на самом деле есть сила трения ведущих колёс о дорогу). В этом случае
— «сила тяги» двигателя автомобиля (которая на самом деле есть сила трения ведущих колёс о дорогу). В этом случае ![]() , и мы получаем просто:
, и мы получаем просто:
![]()
