Закон сохранения импульса

Главная

›

Материалы ›

Физика ›

Механическое движение. Механика ›

Закон сохранения импульса

›

Выбирай среди 25000+ репетиторов из больше 100 предметов

Найти репетитора

Импульс системы тел

Начнём с простой ситуации системы двух тел. А именно, пусть имеются тело 1 и тело 2 с импульсами $\vec{p_1}$ и $\vec{p_2}$ соответственно. Импульс $\vec{p}$ системы данных тел — это векторная сумма импульсов каждого тела:

$\vec{p} = \vec{p_1} + \vec{p_2}.$

Оказывается, для импульса системы тел имеется формула, аналогичная второму закону Ньютона в виде $\frac{d \vec{p} }{ d t } = \vec{F} .$ Давайте выведем эту формулу.

Все остальные объекты, с которыми взаимодействуют рассматриваемые нами тела 1 и 2, мы будем называть внешними телами. Силы, с которыми внешние тела действуют на тела 1 и 2, называем внешними силами. Пусть $\vec{F}_1$ — результирующая внешняя сила, действующая на тело 1. Аналогично $\vec{F}_2$ — результирующая внешняя сила, действующая на тело 2 (рис. 1).

Рисунок 1. Система двух телКроме того, тела 1 и 2 могут взаимодействовать друг с другом. Пусть тело 2 действует на тело 1 с силой $\vec{T}$ . Тогда тело 1 действует на тело 2 с силой $\vec{T}_0$ . По третьему закону Ньютона силы $\vec{T}$ и $\vec{T}_0$ равны по модулю и противоположны по направлению: $\vec{T}_0 = -\vec{T}$ . Силы $\vec{T}$ и $\vec{T}_0$ —
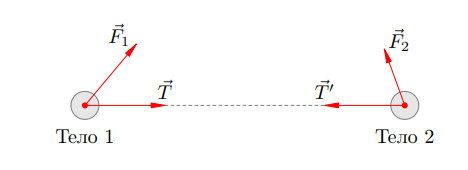
это внутренние силы, действующие в системе.

Запишем для каждого тела 1 и 2 второй закон Ньютона в форме $\frac{d \vec{p} }{ d t } = \vec{F} .$ :

(1) $\begin{equation*} \frac{d\vec{p}_1}{d t} = \vec{F}_1 + \vec{T} , \end{equation*}$

(2) $\begin{equation*} \frac{d\vec{p}_2}{d t} = \vec{F}_2 + \vec{T}_0. \end{equation*}$

Сложим равенства (1) и (2):

$\frac{d\vec{p}_1}{d t} + \frac{d\vec{p}_2}{d t} = \vec{F}_1 + \vec{F}_2 + \vec{T} + \vec{T}_0 .$

В левой части полученного равенства стоит сумма производных, равная производной суммы векторов $\vec{p}_1$ и $\vec{p}_2$ . В правой части имеем $\vec{T} + \vec{T}_0 = \vec{0}$ в силу третьего закона Ньютона:

$\frac{d(\vec{p}_1 + \vec{p}_2)}{d t} = \vec{F}_1 + \vec{F}_2 .$

Но $\vec{p}_1 + \vec{p}_2 = \vec{p}$ — это импульс системы тел 1 и 2. Обозначим также $\vec{F}_1 + \vec{F}_2 = \vec{F}_{vn}$ — это результирующая внешних сил, действующих на систему. Получаем:

(3) $\begin{equation*} \frac{d\vec{p}}{d t} = \vec{F}_{vn} \end{equation*}$

Таким образом, скорость изменения импульса системы тел есть равнодействующая внешних сил, приложенных к системе. Равенство (3), играющее роль второго закона Ньютона для системы тел, мы и хотели получить.
Формула (3) была выведена для случая двух тел. Теперь обобщим наши рассуждения на случай произвольного количества тел в системе.

Найди репетитора по физики

Выбери преподавателя для подготовки к экзаменам и контрольным работам

Импульсом системы тел называется векторная сумма импульсов всех тел, входящих в систему. Если система состоит из $N$ тел, то импульс этой системы равен:

$\vec{p} = \vec{p}_1 + \vec{p}_2 + ..... + \vec{p}_N .$

Дальше всё делается совершенно так же, как и выше (только технически это выглядит несколько сложнее). Если для каждого тела записать равенства, аналогичные (1) и (2), а затем все эти равенства сложить, то в левой части мы снова получим производную импульса системы, а в правой части останется лишь сумма внешних сил (внутренние силы, попарно складываясь, дадут нуль ввиду третьего закона Ньютона). Поэтому равенство (3) останется справедливым и в общем случае.

Закон сохранения импульса

Система тел называется замкнутой, если действия внешних тел на тела данной системы или пренебрежимо малы, или компенсируют друг друга. Таким образом, в случае замкнутой системы тел существенно лишь взаимодействие этих тел друг с другом, но не с какими-либо другими телами.

Равнодействующая внешних сил, приложенных к замкнутой системе, равна нулю: $\vec{F}_{vn} = \vec{0}$ . В этом случае из (3) получаем:

$\frac{d \vec{p}}{dt} = \vec{0}.$

Но если производная вектора обращается в нуль (скорость изменения вектора равна нулю), то сам вектор не меняется со временем:

$\vec{p} = const .$

Закон сохранения импульса. Импульс замкнутой системы тел остаётся постоянным с течением времени при любых взаимодействиях тел внутри данной системы.

Простейшие задачи на закон сохранения импульса решаются по стандартной схеме, которую мы сейчас покажем.

Задача. Тело массы $m_1 = 800$ г движется со скоростью $v_1 = 3$ м/с по гладкой горизонтальной поверхности. Навстречу ему движется тело массы $m_2 = 200$ г со скоростью $v_2 = 13$ м/с. Происходит абсолютно неупругий удар (тела слипаются). Найти скорость тел после удара.
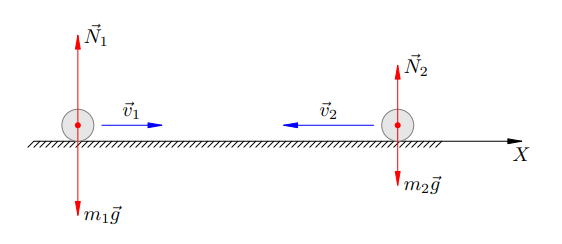
Решение. Ситуация изображена на рисунке 2. Ось X направим в сторону движения первого тела.

Рисунок 2. К задачеПоскольку поверхность гладкая, трения нет. Поскольку поверхность горизонтальная, а движение происходит вдоль неё, сила тяжести и реакция опоры уравновешивают друг друга:

$m_1\vec{g} + \vec{N}_1 = \vec{0}, m_2 \vec{g} + \vec{N}_2 = \vec{0}.$

Таким образом, векторная сумма сил, приложенных к системе данных тел, равна нулю. Это значит, что система тел замкнута. Стало быть, для неё выполняется закон сохранения импульса (обозначим импульс до удара как $\vec{p}_s$ и после удара как $\vec{p}_f$ ):