Закон збереження імпульсу

Головна

›

Матеріали ›

Фізика ›

Механічний рух. Механіка ›

Закон збереження імпульсу

›

Обирай серед 25000+ репетиторів з понад 100 предметів

Знайти репетитора

Імпульс системи тіл

Почнемо з простої ситуації системи двох тіл. А саме, нехай є тіло 1 і тіло 2 з імпульсами $\vec{p_1}$ і $\vec{p_2}$ відповідно. Імпульс $\vec{p}$ системи даних тіл – це векторна сума імпульсів кожного тіла:

$\vec{p} = \vec{p_1} + \vec{p_2}.$

Виявляється, для імпульсу системи тіл є формула, аналогічна до другого закону Ньютона у вигляді $\frac{d \vec{p}}{d t} = \vec{F}.$ Давайте виведемо цю формулу.

Знайди репетитора з фізики

Обери викладача для підготовки до іспитів та контрольних робіт

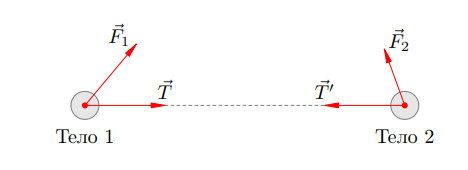
Всі інші об’єкти, з якими взаємодіють тіла 1 і 2, які ми розглядаємо, ми будемо називати зовнішніми тілами. Сили, з якими зовнішні тіла діють на тіла 1 і 2, називаємо зовнішніми силами. Нехай $\vec{F}_1$ – результуюча зовнішня сила, що діє на тіло 1. Аналогічно $\vec{F}_2$ – результуюча зовнішня сила, що діє на тіло 2 (рис. 1).

Рисунок 1. Система двох тіл
Крім того, тіла 1 і 2 можуть взаємодіяти один з одним. Нехай тіло 2 діє на тіло 1 з силою $\vec{T}$ . Тоді тіло 1 діє на тіло 2 з силою $\vec{T}_0$ . За третім законом Ньютона сили $\vec{T}$ і $\vec{T}_0$ рівні по модулю і протилежні за напрямком: $\vec{T}_0 = - \vec{T}$ . Сили $\vec{T}$ і $\vec{T}_0$ –
це внутрішні сили, що діють в системі.

Запишемо для кожного тіла 1 і 2 другий закон Ньютона в формі $\frac{d \vec{p}}{d t} = \vec{F}.$ :

(1) $\begin{equation*} \frac{d\vec{p}_1}{d t} = \vec{F}_1 + \vec{T} , \end{equation*}$

(2) $\begin{equation*} \frac{d\vec{p}_2}{d t} = \vec{F}_2 + \vec{T}_0. \end{equation*}$

Складемо рівності (1) і (2):

$\frac{d\vec{p}_1}{d t} + \frac{d\vec{p}_2}{d t} = \vec{F}_1 + \vec{F}_2 + \vec{T} + \vec{T}_0 .$

У лівій частині отриманого рівності стоїть сума похідних, що дорівнює похідною суми векторів $\vec{p}_1$ і $\vec{p}_2$ . У правій частині маємо $\vec{T} + \vec{T}_0 = \vec{0}$ в силу третього закону Ньютона:

$\frac{d (\vec{p}_1 + \vec{p}_2)}{d t} = \vec{F}_1 + \vec{F}_2.$

Але $\vec{p}_1 + \vec{p}_2 = \vec{p}$ – це імпульс системи тіл 1 і 2. Позначимо також $\vec{F}_1 + \vec{F}_2 = \vec{F}_{vn}$ – це результуюча зовнішніх сил, що діють на систему. отримуємо:

(3) $\begin{equation*} \frac{d\vec{p}}{d t} = \vec{F}_{vn} \end{equation*}$

Таким чином, швидкість зміни імпульсу системи тіл є рівнодіюча зовнішніх сил, прикладених до системи. Рівність (3), що грає роль другого закону Ньютона для системи тіл, ми і хотіли отримати.
Формула (3) була виведена для випадку двох тіл. Тепер узагальнимо наші міркування на випадок довільної кількості тіл в системі.

Імпульсом системи тіл називається векторна сума імпульсів всіх тіл, що входять в систему. Якщо система складається з $N$ тіл, то імпульс цієї системи дорівнює:

$\vec{p} = \vec{p}_1 + \vec{p}_2 + ..... + \vec{p}_N .$

Далі все робиться абсолютно так само, як і вище (тільки технічно це виглядає дещо складніше). Якщо для кожного тіла записати рівності, аналогічні (1) і (2), а потім всі ці рівності скласти, то в лівій частині ми знову отримаємо похідну імпульсу системи, а в правій частині залишиться лише сума зовнішніх сил (внутрішні сили, попарно складався, дадуть нуль зважаючи третього закону Ньютона). Тому рівність (3) залишиться справедливим і в загальному випадку.

Закон збереження імпульсу

Система тіл називається замкнутою, якщо дії зовнішніх тіл на тіла даної системи або нехтовно малі, або компенсують один одного. Таким чином, в разі замкнутої системи тіл істотними є лише взаємодія цих тіл один з одним, але не з будь-якими іншими тілами.

Рівнодіюча зовнішніх сил, прикладених до замкнутій системі, дорівнює нулю: $\vec{F}_{vn} = \vec{0}$ . В цьому випадку з (3) отримуємо:

$\frac{d \vec{p}}{dt} = \vec{0}.$

Але якщо похідна вектора звертається в нуль (швидкість зміни вектора дорівнює нулю), то сам вектор не змінюється з часом:

$\vec{p} = const.$

Закон збереження імпульсу. Імпульс замкнутої системи тіл залишається незмінним з плином часу при будь-яких взаємодіях тіл всередині даної системи.

Найпростіші задачі на закон збереження імпульсу вирішуються за стандартною схемою, яку ми зараз покажемо.

Завдання. Тіло маси $m_1 = 800$ г рухається зі швидкістю $v_1 = 3$ м/с по гладкій горизонтальній поверхні. Назустріч йому рухається тіло маси $m_2 = 200$ г зі швидкістю $v_2 = 13$ м/с. Відбувається абсолютно непружних удар (тіла злипаються). Знайти швидкість тіл після удару.
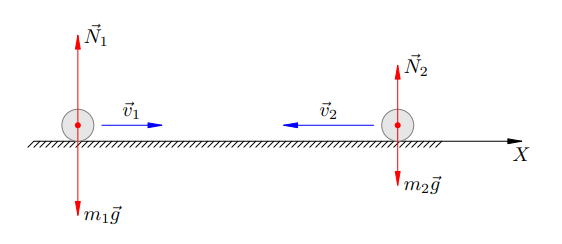
Рішення. Ситуація зображена на рисунку 2. Вісь X направимо в бік руху першого тіла.

Рисунок 2. До задачіОскільки поверхня гладка, тертя немає. Оскільки поверхня горизонтальна, а рух відбувається вздовж неї, сила тяжіння і реакція опори врівноважують один одного:

$m_1\vec{g} + \vec{N}_1 = \vec{0}, m_2 \vec{g} + \vec{N}_2 = \vec{0}.$

Таким чином, векторна сума сил, прикладених до системи даних тіл, дорівнює нулю. Це означає, що система тел замкнута. Стало бути, для неї виконується закон збереження імпульсу (позначимо імпульс до удару як $\vec{p}_s$ і після удару як $\vec{p}_f$ ):