Второй и третий законы Ньютона
Взаимодействие тел можно описывать с помощью понятия силы. Сила — это векторная величина, являющаяся мерой воздействия одного тела на другое. Будучи вектором, сила характеризуется модулем (абсолютной величиной) и направлением в пространстве. Кроме того, важна точка приложения силы: одна и та же по модулю и направлению сила, приложенная в разных точках протяжённого тела, может оказывать различное воздействие. Так, если взяться за обод велосипедного колеса и потянуть по касательной к ободу, то колесо начнёт вращаться. Если же тянуть вдоль радиуса, никакого вращения не будет.
Принцип суперпозиции
Опыт показывает, что если на данное тело действуют несколько других тел, то соответствующие силы складываются как векторы. Более точно, справедлив принцип суперпозиции.Принцип суперпозиции сил. Пусть на тело действуют силы ![]() . Если заменить их одной силой
. Если заменить их одной силой ![]() , то результат воздействия не изменится. Сила
, то результат воздействия не изменится. Сила ![]() называется равнодействующей сил
называется равнодействующей сил ![]() или результирующей силой.
или результирующей силой.
Второй закон Ньютона Если равнодействующая сил, приложенных к телу, равна нулю (то есть воздействия других тел компенсируют друг друга), то в силу первого закона Ньютона найдутся такие системы отсчёта (называемые инерциальными), в которых движение тела будет равномерным и прямолинейным. Но если равнодействующая не обращается в нуль, то в инерциальной системе отсчёта у тела появится ускорение. Количественную связь между ускорением и силой даёт второй закон Ньютона.
Второй закон Ньютона.
Произведение массы тела на вектор ускорения есть равнодействующая всех сил, приложенных к телу: ![]() .
.

Подчеркнём, что второй закон Ньютона связывает векторы ускорения и силы. Это означает, что справедливы следующие утверждения:
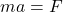 , где
, где  — модуль ускорения,
— модуль ускорения, 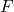 — модуль равнодействующей силы.
— модуль равнодействующей силы.- Вектор ускорения сонаправлен с вектором равнодействующей силы, так как масса тела положительна.
Например, если тело равномерно движется по окружности, то его ускорение направлено к центру окружности. Стало быть, к центру окружности направлена и равнодействующая всех сил, приложенных к телу.
Второй закон Ньютона справедлив не в любой системе отсчёта. Вспомним шатающегося наблюдателя (раздел «Первый закон Ньютона»): относительно него дом движется с ускорением, хотя равнодействующая всех сил, приложенных к дому, равна нулю. Второй закон Ньютона выполняется лишь в инерциальных системах отсчёта, факт существования которых устанавливается первым законом Ньютона.
Третий закон Ньютона
Опыт показывает, что если тело А действует на тело В, то и тело В действует на тело А. Количественную связь между действиями тел друг на друга даёт третий закон Ньютона («действие равно противодействию»).
Третий закон Ньютона. Два тела действуют друг на друга с силами, равными по модулю
и противоположными по направлению. Эти силы имеют одну и ту же физическую природу и направлены вдоль прямой, соединяющей их точки приложения.
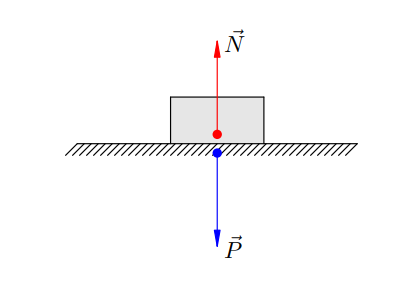
Например, если карандаш действует на стол с силой ![]() , направленной вниз, то стол действует на карандаш с силой
, направленной вниз, то стол действует на карандаш с силой ![]() , направленной вверх (Смотреть рисунок). Эти силы равны по абсолютной величине.
, направленной вверх (Смотреть рисунок). Эти силы равны по абсолютной величине.
![]()
Силы ![]() и
и ![]() , как видим, приложены к разным телам и поэтому не могут уравновешивать друг друга (нет смысла говорить об их равнодействующей).
, как видим, приложены к разным телам и поэтому не могут уравновешивать друг друга (нет смысла говорить об их равнодействующей).
Как найти закон движения?
Законы Ньютона позволяют решить основную задачу механики — найти закон движения тела.
В общих чертах схема действий такова.
- Записываем второй закон Ньютона:
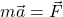 . С учётом того, что ускорение есть втораяпроизводная радиус-вектора, второй закон Ньютона приобретает вид:
. С учётом того, что ускорение есть втораяпроизводная радиус-вектора, второй закон Ньютона приобретает вид:
![Rendered by QuickLaTeX.com \[m\frac{d^2\vec{r}}{dt^2} = \vec{F}.\]](https://repetitor.org.ua/tpl/ql-cache/quicklatex.com-3d57779d3e10c5df982687d2d6d7a037_l3.png)
Необходимо также добавить начальные условия: в начальный момент времени
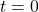 имеем
имеем 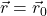 и
и 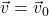 . Начальные значения радиус-вектора и скорости тела предполагаются известными — иначе движение тела нельзя будет описать однозначно. Разумеется, должна быть известна и правая часть равенства, указанного выше — равнодействующая
. Начальные значения радиус-вектора и скорости тела предполагаются известными — иначе движение тела нельзя будет описать однозначно. Разумеется, должна быть известна и правая часть равенства, указанного выше — равнодействующая 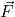 всех сил, приложенных к телу.
всех сил, приложенных к телу. - Второй закон Ньютона, в указанном выше виде, является дифференциальным уравнением. Это уравнение нужно проинтегрировать, то есть найти неизвестную функцию
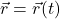 по известной второй производной этой функции. Выполнив интегрирование, мы и определим закон движения.
по известной второй производной этой функции. Выполнив интегрирование, мы и определим закон движения.
Однако легко сказать — «выполнив интегрирование». Сила ![]() может зависеть от координат и скорости тела, а также от времени, вследствие чего интегрирование дифференциального уравнения
может зависеть от координат и скорости тела, а также от времени, вследствие чего интегрирование дифференциального уравнения ![]() окажется весьма сложной задачей. Во многих практических ситуациях такая задача доступна лишь компьютеру.
окажется весьма сложной задачей. Во многих практических ситуациях такая задача доступна лишь компьютеру.
Вот почему центральное место в школьной механике занимает равноускоренное движение: оно происходит под действием постоянной силы, и в этом простейшем случае уравнение ![]() интегрируется элементарно.Имеем:
интегрируется элементарно.Имеем:
![]()
где \vec{a} — постоянный вектор. Интегрируя один раз, с учётом начальных условий получим:
![]()
Теперь интегрируем второй раз:
![]()
Получился уже известный вам закон равноускоренного движения.
Механика, основанная на законах Ньютона, называется классической механикой. Классическая механика, однако, имеет ограниченную область применимости. В рамках классической механики хорошо описывается движение не очень маленьких тел с не очень большими скоростями. При описании атомов и элементарных частиц на замену классической механике приходит квантовая механика. Движение объектов со скоростями, близкими к скорости света, происходит по законам теории относительности.
