Статика твёрдого тела

Статика изучает равновесие тел под действием приложенных к ним сил. Равновесие — это состояние тела, при котором каждая его точка остаётся всё время неподвижной в некоторой инерциальной системе отсчёта. Условием равновесия материальной точки является равенство нулю равнодействующей (т. е. векторной суммы) всех сил, приложенных к точке. В этом случае наша точка будет двигаться равномерно и прямолинейно в произвольной инерциальной системе отсчёта. Значит, система отсчёта, связанная с точкой, также будет инерциальной, и в ней точка будет покоиться.
В случае твёрдого тела ситуация сложнее. Прежде всего, важно учитывать точку приложения каждой силы.

• Сила тяжести приложена в центре тяжести тела. Для тела простой формы центр тяжести совпадает с центром симметрии.
• Силы упругости и трения приложены в точке или в плоскости контакта тела с соприкасающимся телом.

Прямая линия, проходящая через точку приложения вдоль вектора силы, называется линией действия силы. Оказывается, точку приложения силы можно переносить вдоль линии
её действия — от этого механическое состояние тела не изменится (в частности, равновесие не
нарушится).
Для равновесия твёрдого тела недостаточно потребовать равенства нулю векторной суммы
всех приложенных к телу сил.

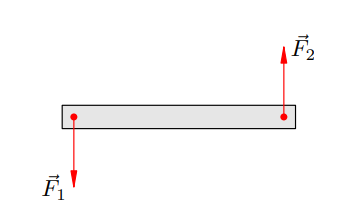
В качестве примера рассмотрим пару сил — так называются две равные по модулю противоположно направленные силы, линии действия которых не совпадают. Пусть пара сил и приложена к твёрдому стержню (Рисунок 1).

Рисунок 1. Пара силВекторная сумма этих сил равна нулю. Но стержень покоиться не будет: он начнёт вращаться. В данном случае не выполнено второе условие равновесия твёрдого тела. Чтобы его сформулировать, нужно ввести понятие момента силы.
Как должна быть направлена линия действия силы, чтобы тело стало вращаться вокруг неподвижной оси? Для начала заметим следующее.

• Если линия действия силы параллельна данной оси, то вращения не будет.
• Если линия действия силы пересекает данную ось, то вращения не будет.

В каждом из этих случаев действие силы вызывает лишь деформацию твёрдого тела. Чтобы началось вращение, линия действия силы и ось вращения должны быть скрещивающимися прямыми. Без ограничения общности можно считать эти прямые перпендикулярными друг другу. Мы всегда можем этого добиться, разложив силу на две составляющие — параллельную и перпендикулярную оси вращения — и отбросив параллельную составляющую как не вызывающую
вращения. Поэтому везде далее мы считаем, что все силы, действующие на тело, перпендикулярны оси вращения.

Момент силы

Плечо силы — это расстояние от оси вращения до линия действия силы (т. е. длина общего
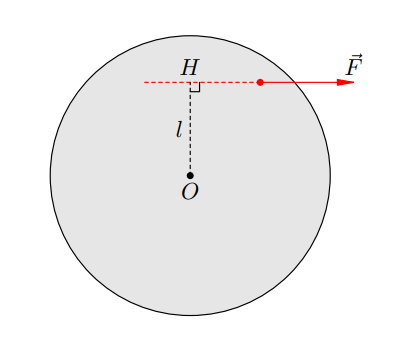
перпендикуляра к двум этим прямым). В качестве примера на Рисунке 2 изображён диск, к которому приложена сила . Ось вращения перпендикулярна плоскости чертежа и проходит через точку O. Плечом силы является
величина = OH, где H — основание перпендикуляра, опущенного из точки O на линию действия силы.

Рисунок 2. Плечо силы
Момент силы относительно оси вращения — это произведение силы на плечо:

   

Чтобы учесть также направление вращения, вызываемого действием силы, моменту силы приписывают знак. Именно, момент силы считается положительным, если сила стремится поворачивать тело против часовой стрелки, и отрицательным, если по часовой стрелке.

Условия равновесия

Если тело имеет неподвижную ось вращения и если алгебраическая сумма моментов всех сил относительно этой оси обращается в нуль, то тело будет находиться в равновесии. Это так называемое правило моментов. Оказывается, что в этом случае обращается в нуль алгебраическая сумма моментов всех сил относительно любой другой оси, параллельной оси вращения.

В общем случае, когда твёрдое тело может совершать как поступательное, так и вращательное движение, мы имеем два условия равновесия.

1. Равна нулю векторная сумма всех сил, приложенных к телу.
2. Равна нулю алгебраическая сумма моментов всех сил, приложенных к телу, относительно данной оси вращения или любой другой оси, параллельной данной.

Так, в примере на Рисунке 1 алгебраическая сумма моментов пары сил не обращается нуль (оба момента положительны). Поэтому стержень не находится в равновесии. При решении задач удобно использовать сформулированные выше условия равновесия в следующем виде.

1. Силы уравновешены вдоль любой оси.
2. Суммарный момент сил, вращающих тело в одну сторону, равен суммарному моменту сил, вращающих тело в другую сторону.