Робота. Потужність.
Робота
Нехай на тіло діє постійна сила ![]() і тіло, рухаючись прямолінійно по горизонтальній поверхні, зробило переміщення
і тіло, рухаючись прямолінійно по горизонтальній поверхні, зробило переміщення ![]() . Сила
. Сила ![]() не обов’язково є безпосередньою причиною переміщення (так, сила тяжіння не є безпосередньою причиною переміщення шафи, яку пересувають по кімнаті).
не обов’язково є безпосередньою причиною переміщення (так, сила тяжіння не є безпосередньою причиною переміщення шафи, яку пересувають по кімнаті).
Припустимо спочатку, що вектори сили і переміщення співнаправлені (рис. 1, решта сили, що діють на тіло, не вказані).
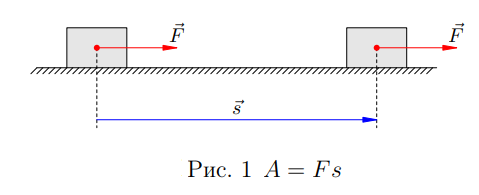
У цьому простому випадку робота ![]() визначається як добуток модуля сили на модуль
визначається як добуток модуля сили на модуль
переміщення:
(1) ![]()
Одиницею вимірювання роботи служить джоуль (Дж): Дж = Н · м. Таким чином, якщо під дією сили 1 Н тіло переміщається на 1 м, то сила здійснює роботу 1 Дж.

Робота сили, перпендикулярної переміщенню, за визначенням вважається рівною нулю. Так, в даному випадку сила тяжіння і сила реакції опори не здійснюють роботи.
Нехай тепер вектор сили утворює з вектором переміщення гострий кут ![]() (рис. 2).
(рис. 2).
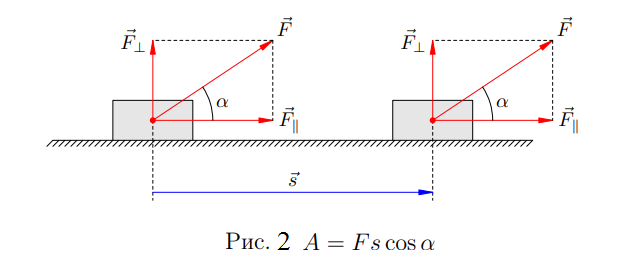
Розкладемо силу ![]() на дві складові:
на дві складові: ![]() (паралельну переміщенню) і
(паралельну переміщенню) і ![]() (перпендикулярну переміщенню). Роботу здійснює тільки
(перпендикулярну переміщенню). Роботу здійснює тільки ![]() . Тому для роботи сили
. Тому для роботи сили ![]() отримуємо:
отримуємо:
![]() Отже,
Отже,
(2) ![]()
Якщо вектор сили утворює з вектором переміщення тупий кут ![]() , то робота, як і раніше визначається формулою (2). У цьому випадку робота виявляється негативною.
, то робота, як і раніше визначається формулою (2). У цьому випадку робота виявляється негативною.
Наприклад, робота сили тертя ковзання, що діє на тіло в розглянутих ситуаціях, буде негативною, так як сила тертя спрямована протилежно переміщенню. У цьому випадку маємо: ![]() = 180◦,
= 180◦, ![]() , і для роботи сили тертя отримуємо:
, і для роботи сили тертя отримуємо:
![]()
де ![]() – маса тіла,
– маса тіла, ![]() – коефіцієнт тертя між тілом і опорою.
– коефіцієнт тертя між тілом і опорою.
Співвідношення (2) означає, що робота є скалярним твором векторів сили і переміщення:
![]()
Це дозволяє обчислювати роботу через координати даних векторів:
![]()
Нехай на тіло діють кілька сил ![]() і
і ![]() – рівнодіюча цих сил. Для роботи сили
– рівнодіюча цих сил. Для роботи сили ![]() маємо:
маємо:
![]()
або
![]()
де ![]() – роботи сил
– роботи сил ![]()
Отже, рівнодіюча робота прикладених до тіла сил дорівнює сумі робіт кожної сили окремо.
Потужність
Часто має значення швидкість, з якою відбувається робота. Скажімо, на практиці важливо знати, яку роботу зможе виконати даний пристрій за фіксований час.
Потужність – це величина, що характеризує швидкість здійснення роботи. Потужність ![]()
є відношення роботи ![]() до часу
до часу ![]() , за яке ця робота здійснена:
, за яке ця робота здійснена:
![]()
Потужність вимірюється у Ватах (Вт). 1 Вт = 1 Дж/с, тобто 1 Вт – це така потужність, при якій робота в 1 Дж відбувається за 1 с.
Припустимо, що сили, що діють на тіло, врівноважені, і тіло рухається рівномірно і прямолінійно зі швидкістю ![]() . У цьому випадку існує корисна формула для потужності, що розвивається однієї з діючих сил
. У цьому випадку існує корисна формула для потужності, що розвивається однієї з діючих сил ![]() .
.
За час ![]() тіло зробить переміщення
тіло зробить переміщення ![]() Робота сили
Робота сили ![]() буде дорівнювати:
буде дорівнювати:
![]()
Звідси отримуємо потужність:
![]()
або
![]()
де ![]() – кут між векторами сили і швидкості.
– кут між векторами сили і швидкості.
Найбільш часто ця формула використовується в ситуації, коли ![]() – «сила тяги» двигуна автомобіля (яка насправді є сила тертя коліс об дорогу). В цьому випадку
– «сила тяги» двигуна автомобіля (яка насправді є сила тертя коліс об дорогу). В цьому випадку ![]() , і ми отримуємо просто:
, і ми отримуємо просто:
![]()
