Потенціальна енергія - Дистанційна підтримка освіти школярів

Головна

›

Матеріали ›

Фізика ›

Механічний рух. Механіка ›

Потенціальна енергія

›

Обирай серед 25000+ репетиторів з понад 100 предметів

Знайти репетитора

Потенційна енергія тіла поблизу поверхні Землі

Розглянемо тіло маси $m$ , що знаходиться на деякій висоті над поверхнею Землі. Висоту вважаємо значно меншою за радіус Землі. Зміною сили тяжіння в процесі переміщення тіла нехтуємо.

Якщо тіло знаходиться на висоті $h$ , то потенціальна енергія тіла за визначенням дорівнює:

$W = m g h,$

де $g$ – прискорення вільного падіння поблизу поверхні Землі. Висоту не обов’язково відраховувати від поверхні
Землі. Як ми побачимо нижче (формули (1), (2)), фізичним змістом володіє не сама по собі потенціальна енергія, а її зміна. А зміна потенціальної енергії не залежить від точки відліку. Вибір нульового рівня потенційної енергії в конкретному завданні диктується виключно міркуваннями зручності.

Знайдемо роботу, що здійснюються силою тяжіння при переміщенні тіла. Припустимо, що тіло
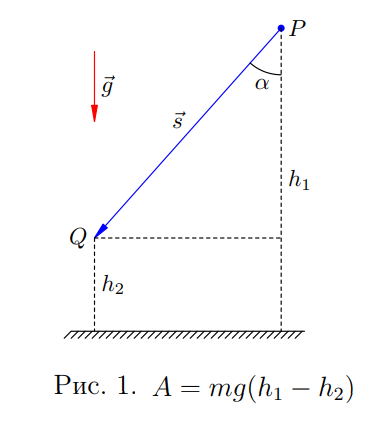
переміщається по прямій з точки P, що знаходиться на висоті $h_1$ , в точку Q, що знаходиться на висоті $h_2$ (рис. 1).

Кут між силою тяжіння $m \vec{g}$ і переміщенням тіла $\vec{s}$ позначимо $\alpha$ . Для роботи сили тяжіння отримаємо:

$A = m\vec{g} \vec{s} = m g s cos \alpha.$

Але, як видно з рис. 1, $s cos \alpha = h_1 - h_2$ . Тому

$A = m g (h_1 − h_2) = m g h_1 - m g h_2,$

або

(1) $\begin{equation*} A = W_1 - W_2. \end{equation*}$

З огляду на, що $W_1 - W_2 = - (W_2 - W_1) = - \Delta W$ , маємо також:

(2) $\begin{equation*} A = - \Delta W. \end{equation*}$

Можна довести, що формули (1) і (2) справедливі для будь-якої траєкторії, по якій тіло переміщається з точки P в точку Q, а не тільки для прямолінійного відрізка.

Знайди репетитора з фізики

Обери викладача для підготовки до іспитів та контрольних робіт

Робота сили тяжіння не залежить від форми траєкторії, по якій переміщається тіло, і дорівнює різниці значень потенційної енергії в початковій і кінцевій точках траєкторії. Іншими словами, робота сили тяжіння завжди дорівнює зміні потенційної енергії з протилежним знаком. Зокрема, робота сили тяжіння по будь-якому замкнутому шляху дорівнює нулю.
Сила називається консервативною , якщо при переміщенні тіла робота цієї сили не залежить
від форми траєкторії, а визначається тільки початковим і кінцевим положенням тіла. Сила тяжіння, таким чином, є консервативною. Робота консервативної сили по будь-якому замкнутому шляху дорівнює нулю. Тільки в разі консервативної сили можливо ввести таку величину, як потенціальна енергія.

Потенціальна енергія деформованої пружини

Розглянемо пружину жорсткості $k$ . Початкова деформація пружини дорівнює $x_1$ . Припустимо, що пружина деформується до деякої кінцевої величини деформації $x_2$ . Чому дорівнює при цьому робота сили пружності пружини?
В даному випадку силу на переміщення не перемножиш, так як сила пружності змінюється в процесі деформації пружини. Для знаходження роботи змінної сили потрібно інтегрування. Ми не будемо наводити тут виведення, а відразу випишемо кінцевий результат.

Виявляється, сила пружності пружини також є консервативною. Її робота залежить лише від величин $x_1$ , $x_2$ і визначається формулою:

$A = \frac{kx^2_1}{2} - \frac{kx^2_2}{2}.$

величина

$W = \frac{kx^2}{2}$

називається потенційною енергією деформованої пружини ( $x$ – величина деформації). отже,

$A = W_1 - W_2 = - \Delta W,$

що повністю аналогічно формулам (1) і (2).