Асоціація
репетиторів
України RU |  UA
Питання? Телефонуйте нам:

Штучні супутники Землі

Обирай репетитора фізики, щоб розібратися в темі

Штучні супутники, що обертаються навколо Землі – це одна із найвідоміших сучасних технологій. (Рис. 1). А тому у кожного виникає питання: як вони залишаються на орбіті, і як визначаються їх орбіти? Ми використаємо закони Ньютона і закон гравітації, щоб знайти на це відповіді. До того ж рух планет можна описувати за допомогою схожих міркувань.
Телескоп Хабл

Рисунок 1. Космічний телескоп Хабл один з найбільших штучних супутників виведених на орбіту. Його вага 11 тонн, а довжина 13,5 м.

Для початку уявімо собі мотоцикліста, який, розігнавшись по горизонтальній поверхні, стрибає з обриву. Якщо він виживе і повторить експеримент з розігнавшись ще швидше, він приземлиться далі, ніж першого разу. Уявімо собі, що мотоцикліст розігнався до такої швидкості, що викривлення Землі стало суттєвим. В такому випадку, він буде падати, а земля буде вигинатися під ним. Якщо ж він буде їхати з досить високою швидкістю і точка “запуску” буде досить високо, щоб можна було не зачіпати вершин гір, він зможе літати навколо Землі не приземляючись.

Навчайся разом з Репетиторами України
Обери викладача для підготовки до іспитів та контрольних робіт
Шукати репетитора

На рисунку 2 показані варіанти цих “запусків”. Ми запускаємо снаряд з точки А вздовж прямої AB, дотичний до поверхні землі. Траєкторії з 1 по 7 показують як змінюється траєкторія залежно від початкової швидкості. На траєкторіях з 3 по 5 снаряд не падає на землю і стає супутником. Якщо немає сили, що сповільнює снаряд, то його швидкість при поверненні в точку A, дорівнює його початковій швидкості і він повторює свій рух до бескінечності.
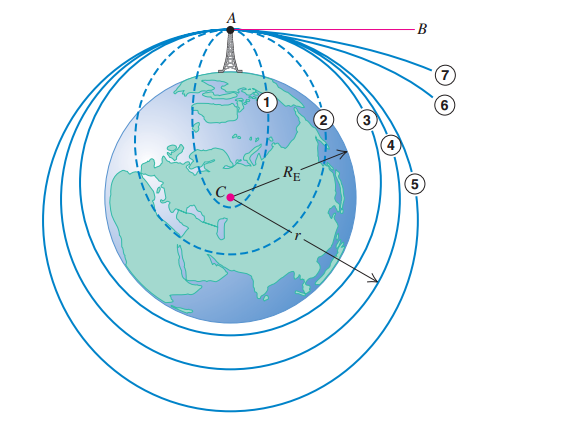
Траектории спутников

Рисунок 2. Траєкторії супутників в залежності від початкової швидкості

Траєкторії з 1 по 5 замикаються і називаються замкнутими орбітами. Всі замкнуті орбіти – це еліпси або сегменти еліпсів; Траєкторія 4 являє собою коло, особливий випадок еліпса. Траєкторії 6 і 7 є відкритими орбітами. Для цих шляхів снаряд ніколи не повертається до його відправної точки і летить все далі від землі.

Супутники: кругові орбіти

Кругова орбіта, показана на рис.2 під номером 4, є найпростішим випадком. Така траєкторія дуже важливий випадок, оскільки багато штучних супутників мають майже кругові орбіти, як і орбіти планет навколо Сонця. Єдина сила, яка діє на супутник на круговій орбіті при русі навколо Землі – це гравітаційна сила притягання Землі, яка спрямована до центру землі, а отже, і до центру орбіти-кола (рис. 3). Це означає, що супутник здійснює рівномірний круговий рух і його швидкість постійна. Супутник не падає на Землю; скоріше він постійно падає навколо землі.
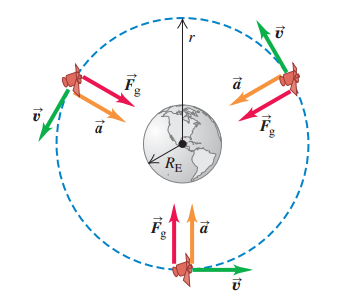
Сила гравитации

На круговій орбіті швидкість супутника якраз не повинна змінюватися для підтримки відстані постійною між супутником і центром Землі. Розглянемо, як знайти постійну швидкість супутника на круговій орбіті. Радіус орбіти r вимірюється від центру Землі; Прискорення супутника має величину a_{rad} = \frac{v^2}{r} і завжди направлене в центр кола. Гравітаційна сила, яка діє на супутник маси m спрямована в тому ж напрямку, що і прискорення:

    \[F_g = \frac{G M m}{r^2},\]

де M – маса Землі.
Згідно з другим законом Ньютона (\vec{F} = m \vec{a}) маємо:

    \[\frac{G M m}{r^2} = \frac{mv^2}{r}\]

Звідси

Рівняння 1

(1)   \begin{equation*} v = \sqrt{\frac{GM}{r}} \end{equation*}

Ця швидкість в літературі називається першою космічною швидкістю.
У формулі (1) немає маси супутника, а це означає, що швидкість супутника не залежить від його маси. Якби ми могли розрізати супутник навпіл, не змінюючи його швидкості, то кожна половинка продовжувала б рухатися з тією ж швидкість, що і цілий супутник.

Астронавт на борту космічної станції теж є супутником Землі, який утримується гравітаційним тяжінням Землі на тій же орбіті, що і станція. Астронавт має ту ж швидкість і прискорення, що і станція, тому ніяка сила не штовхає його до будь-якої зі стінок станції. Людина знаходиться в стані уявної невагомості, як у вільно падаючому ліфті. (Повна невагомість виникне, тільки якщо космонавт буде нескінченно віддалений від будь-яких інших мас, так що гравітаційна сила, що діє на нього, буде дорівнювати нулю.) Дійсно, кожна частина його тіла майже невагома; він нічого не відчуває, притискаючи коліна до живота або голову до плечей.

Удавана невагомість – це не просто особливість кругових орбіт; це відбувається, коли гравітація є єдиною силою, що діє на космічний корабель. Отже, це відбувається для орбіт будь-якої форми, включаючи відкриті орбіти, такі як траєкторії 6 і 7 на рис. 2.

Ми можемо вивести співвідношення між радіусом кругової орбіти і періодом T – часом одного обороту. Швидкість – це відстань, пройдена за один оборот, поділена на період:

Рівняння 2

    \[\begin{eqution} \label{2} v = \frac{2 \pi r}{T} \end{equation}\]

З (2) знаходимо, чому буде дорівнювати T, підставивши значення швидкості з (1):

Рівняння 3

    \[\begin{eqution}\label{3} T = \frac{ 2 \pi r}{v} = 2 \pi r \sqrt{\frac{r}{GM}} = \frac{2 \pi r^{\frac{3}{2}}}{\sqrt{GM}} \end{equation}\]

Рівняння (1) і (3) показують, що більші орбіти відповідають більш повільним швидкостям і більш тривалим періоди. Наприклад, орбіта Міжнародної космічної станції знаходиться далі ніж на 6800 км від центру Землі (400 км над земною поверхнею) з орбітальною швидкістю 7,7 км/с та орбітальним періодом 93 хвилини. В той час як Місячна орбіта Землі знаходиться на набагато більшій відстані з радіусом 384 000 км, і тому має набагато меншу орбітальну швидкість (1,0 км с) і значно довший орбітальний період (27,3 дня).

Оскільки швидкість v на круговій орбіті для заданого радіуса орбіти r визначається за формулою (1), то можна визначити повну механічну енергію супутника.

    \[E = K + U = \frac{mv^2}{2}+(-\frac{GMm}{r}) = \frac{1}{2}m\frac{GM}{r} - \frac{GMm}{r} = - \frac{GMm}{2r}\]

Повна механічна енергія на круговій орбіті негативна і дорівнює половині потенціальної енергії. Збільшення радіусу орбіти r означає збільшення механічної енергії (тобто, повна енергія стає менш негативною). Якщо супутник знаходиться на відносно низькій орбіті, яка перетинається із зовнішніми кордонами земної атмосфери, механічна енергія зменшується через негативну роботу, яка виконується силою опору повітря; в результаті радіус орбіти зменшується до тих пір, поки супутник не впаде на землю або не згорить в атмосфері.
Ми говорили в основному про земні супутники, але ми можемо застосувати той самий аналіз для колового руху будь-якої людини, що знаходиться під дією гравітаційного тяжіння стаціонарного тіла.

Top