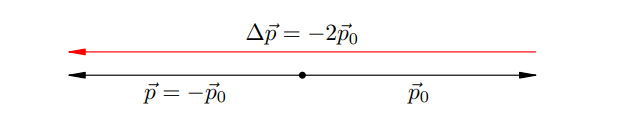Імпульс тіла
Імпульс тіла – це векторна величина, що дорівнює добутку маси тіла на його швидкість:
![]()
Спеціальних одиниць вимірювання імпульсу немає. Розмірність імпульсу – це просто витвір розмірності маси на розмірність швидкості:
Другий закон Ньютона в імпульсної формі
Нехай ![]() – рівнодіюча сил, прикладених до тіла маси
– рівнодіюча сил, прикладених до тіла маси ![]() . Починаємо з звичайного запису другого закону Ньютона:
. Починаємо з звичайного запису другого закону Ньютона:
![]()
З урахуванням того, що прискорення тіла ![]() дорівнює похідній вектора швидкості, другий закон Ньютона переписується наступним чином:
дорівнює похідній вектора швидкості, другий закон Ньютона переписується наступним чином:
![]()
Вносимо константу ![]() під знак похідної:
під знак похідної:
![]()
Як бачимо, в лівій частині вийшла похідна імпульсу:
(1) ![]()
Співвідношення (1) і є нова форма запису другого закону Ньютона.

Другий закон Ньютона в імпульсної формі. Похідна імпульсу тіла є рівнодіюча прикладених до тіла сил.
Можна сказати і так: результуюча сила, що діє на тіло, дорівнює швидкості зміни імпульсу тіла. Похідну у формулі (1) можна замінити на відношення скінченних приростів:
(2) ![]()
В цьому випадку ![]() є середня сила, що діє на тіло протягом інтервалу часу
є середня сила, що діє на тіло протягом інтервалу часу ![]() . чим
. чим
менше величина ![]() , тим ближче відношення
, тим ближче відношення ![]() до похідної
до похідної ![]() , і тим ближче середня сила
, і тим ближче середня сила ![]() до свого миттєвому значенню в даний момент часу.
до свого миттєвому значенню в даний момент часу.
У завданнях, як правило, інтервал часу ![]() досить малий. Наприклад, це може бути час зіткнення м’яча із стінкою, і тоді
досить малий. Наприклад, це може бути час зіткнення м’яча із стінкою, і тоді ![]() – середня сила, що діє на м’яч з боку стінки під час удару.
– середня сила, що діє на м’яч з боку стінки під час удару.
Вектор ![]() в лівій частині співвідношення (2) називається зміною імпульсу за час
в лівій частині співвідношення (2) називається зміною імпульсу за час ![]() . Зміна імпульсу – це різниця кінцевого і початкового векторів імпульсу. А саме, якщо
. Зміна імпульсу – це різниця кінцевого і початкового векторів імпульсу. А саме, якщо ![]() – імпульс тіла в деякий початковий момент часу,
– імпульс тіла в деякий початковий момент часу, ![]() – імпульс тіла через проміжок часу
– імпульс тіла через проміжок часу ![]() , то зміна імпульсу є різниця:
, то зміна імпульсу є різниця:
![]()
Підкреслимо ще раз, що зміна імпульсу – це різниця векторів. Нагадаємо, що при побудові різниці векторів потрібно мпівставити початки обох векторів, з’єднати їх кінці і «вколоти» стрілкою той вектор від якого робиться віднімання.
Нехай, наприклад, м’яч летить перпендикулярно стінці (імпульс перед ударом дорівнює ![]() ) і відскакує назад без втрати швидкості (імпульс після удару дорівнює
) і відскакує назад без втрати швидкості (імпульс після удару дорівнює ![]() ). Незважаючи на те, що імпульс по модулю не змінився
). Незважаючи на те, що імпульс по модулю не змінився ![]() , зміна імпульсу не дорівнює нулю:
, зміна імпульсу не дорівнює нулю:
![]()
Модуль зміни імпульсу, як бачимо, дорівнює подвоєному модулю початкового імпульсу м’яча: ![]()
Перепишемо формулу (2) наступним чином:
(3) ![]()
або, розписуючи зміна імпульсу, як і вище:
![]()
Величина ![]() називається імпульсом сили. Спеціальної одиниці виміру для імпульсу сили немає; розмірність імпульсу сили дорівнює просто добутку різниці сили і часу:
називається імпульсом сили. Спеціальної одиниці виміру для імпульсу сили немає; розмірність імпульсу сили дорівнює просто добутку різниці сили і часу:
(Зверніть увагу, що Н · с є ще однією можливою одиницею виміру імпульсу тіла.)
Словесне формулювання рівняння (3) таке: зміна імпульсу тіла дорівнює імпульсу діючої на тіло сили за даний проміжок часу. Це знову є другий закон Ньютона в імпульсної формі.