Законы Кеплера. Движение планет.

Главная

›

Материалы ›

Физика ›

Механическое движение. Механика ›

Законы кеплера и движение планет

›

Выбирай среди 25000+ репетиторов из больше 100 предметов

Найти репетитора

Слово «планета» происходит от греческого слова, означающего «странник», и действительно планеты постоянно меняют свое положение в небе относительно звезд. Одним из самых великих интеллектуальных достижений 16-го и 17-го веков было осознание того, что Земля это тоже планета, все планеты вращаются вокруг Солнца, и движения планет, наблюдаемое с Земли, может быть использовано для весьма точного определения их орбит.

Первая и вторая из этих идей были опубликованы Николаем Коперником в Польше в 1543 году. Законы, по которым движутся планеты, были выведены между 1601 и 1619 годами немецким астрономом и математиком Йоханнесом Кеплером. Он использовал громадное (по меркам того столетия) количество точных данных о видимых планетарных движениях, собранных его наставником, датский астрономом Тихо Браге. Методом проб и ошибок Кеплер обнаружил три эмпирических закона, которые точно описывали движения планеты:

Каждая планета солнечной системы движется по эллиптической орбите с солнцем в одном из фокусов эллипса.
Каждая планета движется в плоскости, проходящей через центр Солнца, причём за равные промежутки времени радиус-вектор, соединяющий Солнце и планету, заметает собой равные площади.
Периоды вращения планет вокруг Солнца пропорциональны степеням длины большых полуосей их орбит.

Кеплер не знал, почему планеты двигаются таким образом. Три поколения спустя, когда Ньютон обратил свое внимание на движение планет, он обнаружил, что каждый из законов Кеплера может быть выведен. Эти законы следствие законов движения и гравитации Ньютона. Давайте посмотрим, как возникает каждый из законов Кеплера.

Найди репетитора по физики

Выбери преподавателя для подготовки к экзаменам и контрольным работам

Первый закон Кеплера

Сначала рассмотрим эллиптические орбиты, описанные в первом законе Кеплера. Рисунок 1 показывает геометрия эллипса. Самым длинным измерением является главная ось с половиной длины; эта половина длины называется большой полуосью. Сумма расстояний От S до P и от S’ до P одинакова для всех точек эллиптической орбиты. S и S’ — это фокусы эллипса. Солнце находится в точке S, а планета в точке P; мы представляем их в виде точек, потому что их размеры очень малы по сравнению с расстоянием между ними. На другом фокусе ничего нет.

Рисунок 1. Первый закон Кеплера.Расстояние каждого фокуса от центра эллипса равно ea, где e — безразмерное число от 0 до 1 называемое эксцентриситетом. Если эллипс — это круг, то фактические орбиты планет довольно круглые; их эксцентриситеты колеблются от 0,007 для Венеры до 0,206 для Меркурия. У земной орбиты есть две особенные точки: ближайшая к Солнцу — это перигелий, и наиболее удаленная от солнца — афелий.

Ньютон смог показать, что тела, на которое действует сила притяжения, имеют единственно возможные замкнутые орбиты в виде круга или эллипса; он также показав, что открытые орбиты должны быть параболами или
гиперболами. Эти результаты могут быть получены путем прямого применения Законов Ньютона и закона гравитации, вместе с гораздо более сложными дифференциальными уравнениями.

Второй закон Кеплера

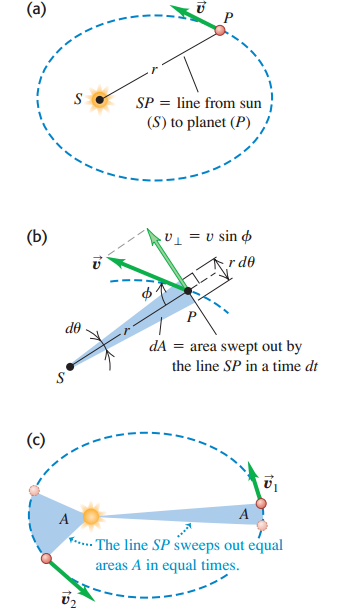
На рисунке 2 показан второй закон Кеплера. Через небольшой интервал времени $d t$ линия, соединяющая солнце S и планету P, поворачивается на угол $d \theta$ . На рис.2(b) видим закрашеный треугольник с высотой $r$ , длиной основания $r d \theta$ и площадью $dA = \frac{1}{2}r^2d \theta$ . Скорость, с которой выметается площадь $\frac{dA}{dt}$ , называется секторной скоростью:

(1) $\begin{equation*} \frac{dA}{dt} = \frac{1}{2}r^2\frac{d\theta}{dt} \end{equation*}$

Рисунок 2. Второй закон Кеплера
Суть второго закона Кеплера заключается в том, что секториальная скорость имеет одинаковое значение во всех точках на орбите. Когда планета находится близко к Солнцу, то значение $r$ — маленькое, а $\frac{d \theta}{dt}$ — большое, а когда планета находится далеко от солнца, то $r$ становится большим, а $\frac{d \theta}{dt}$ — маленьким.

Чтобы увидеть, как второй закон Кеплера следует из законов Ньютона, мы выражаем $\frac{dA}{dt}$ в терминах вектора скорости $\vec{v}$ планеты P. Компонента $\vec{v}$ перпендикулярная радиальной линии будет: $v_{\perp} = v \sin \phi$ . Как показано на рис. 2b перемещение вдоль направления $v_{\perl}$ на протяжении времени $dt$ будет равно $r d\theta$ , поэтому мы также имеем $v_{\perl} = r \frac{d \theta}{dt}$
Подставляя это соотношение в формулу (1), мы находим

(2) $\begin{equation*} \frаc{dA}{dt} = \frac{1}{2} r v \sin \phi \end{equation*}$

Величина $r v \sin \phi$ есть не что иное как векторное произведение $\vec{v} \times \vec{r}$ , домножив которое на $m$ получим момент импульса планеты относительно Солнца $\vec{L} = [\vec{v} \times m \vec{r}]$ . Итак, мы имеем

(3) $\begin{equation*} \frаc{dA}{dt} = \frac{1}{2m} [\vec{v} \times m \vec{r}] = \frac{\vec{L}}{2m} \end{equation*}$

Таким образом, второй закон Кеплера гласит: секториальная скорость постоянна, а из этого следует, что угловой момнет импульса постоянен!

Легко понять, почему момент импульса планеты должен быть постоянным.
Зная, что из менение момент импульса $\vec{L}$ во равно моменту $\vec{M}$ силы гравитации $\vec{F}$ , действующей на планету, имеем:

$\frac{d\vec{L}}{dt} = \vec{M} = \vec{r} \times m\vec{F}.$

В нашей случае, $r$ — это вектор от Солнца до планеты, а сила $\vec{F}$ направлен от планеты к солнцу. Таким образом, эти два вектора всегда лежат вдоль одной и той же линии, и их векторное произведение равно нулю. Отсюда $\frac{d\vec{L}}{dt}$ .
Если угловой момент импульса сохраняется, то такая сила называется центральной силой.

Третий закон Кеплера

Квадраты периодов обращения планет вокруг Солнца относятся, как кубы больших полуосей орбит планет.

$\frac{T^2_1}{T^2_2} = \frac{r^3_1}{r^3_2}$

Из этого следуает, что период спутника или планеты на круговой орбите пропорционален степени $\frac{3}{2}$ от радиуса орбиты. Ньютон смог показать что это же соотношение верно для эллиптической орбиты с заменой радиуса орбиты $r$ на большую полуось $а$ :

$T = \frac{2 \pi a^{\frac{3}{2}}}{\sqrt{GM}}$

Обратите внимание, что период не зависит от эксцентриситета е. Астероид на вытянутой эллиптической орбите с большой главной осью $a$ будет иметь такой же период обращения, что и планета на круговой орбите радиуса $a$ .
Ключевое отличие состоит в том, что астероид движется с разными скоростями в разных точках своей эллиптической орбиты (рис. 2c), в то время как скорость планеты постоянна вокруг своей круговой орбиты.