Закони Кеплера - Видимий рух планет.

Головна

›

Матеріали ›

Фізика ›

Механічний рух. Механіка ›

Закони Кеплера і рух планет

›

Обирай репетитора фізики, щоб розібратися в темі

Знайти репетитора

Слово “планета” походить від грецького слова, що означає “мандрівник”, і дійсно планети постійно змінюють своє положення в небі відносно зір. Одним з найбільш великих інтелектуальних досягнень 16-го і 17-го століть було усвідомлення того, що Земля це теж планета і всі планети обертаються навколо Сонця. Рух планет, що спостерігається з Землі, може бути використаний для досить точного визначення їх орбіт.

Навчайся разом з Репетиторами України

Обери викладача для підготовки до іспитів та контрольних робіт

Перша і друга з цих ідей були опубліковані Миколою Коперником в Польщі в 1543 році. Закони, за якими рухаються планети, були виведені між 1601 і 1619 роками німецьким астрономом і математиком Йоханнесом Кеплером. Він використовував величезну (за мірками того століття) кількість точних даних про спостережувані планетарні рухи, зібрані його наставником, датським астрономом Тихо Браге. Методом спроб і помилок Кеплер виявив три емпіричних закони, які точно описували рух планет:

1. Кожна планета сонячної системи рухається по еліптичній орбіті і в одному з фокусів цього еліпса знаходиться Сонце.
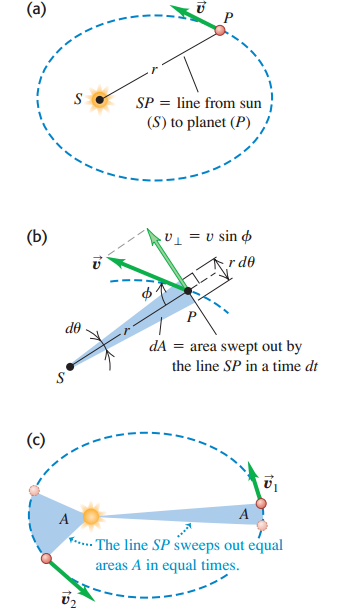
2. Кожна планета рухається в площині, що проходить через центр Сонця, причому за рівні проміжки часу радіус-вектор, що з’єднує Сонце і планету, замітає собою рівні площі.

Періоди обертання планет навколо Сонця пропорційні степеням довжини великих півосей їх орбіт.

Кеплер не знав, чому планети рухаються таким чином. Три покоління по тому, коли Ньютон звернув свою увагу на рух планет, він виявив, що кожен із законів Кеплера може бути виведений. Ці закони є наслідком законів руху Ньютона. Давайте подивимося, як виникає кожен із законів Кеплера.

Перший закон Кеплера

Спочатку розглянемо еліптичні орбіти, описані в першому законі Кеплера. На рисунку 1 зображена геометрія еліпса. Найдовшим виміром є головна вісь з половиною довжини; ця половина довжини називається великою піввіссю. Сума відстаней Від S до P і від S’ до P однакова для всіх точок еліптичної орбіти. S і S’- це фокуси еліпса. Сонце знаходиться в точці S, а планета в точці P; ми представляємо їх у вигляді точок, тому що їх розміри дуже малі в порівнянні з відстанню між ними. В другому фокусі нічого немає.

Рисунок 1. Перший закон Кеплера.
Відстань від кожного фокуса до центру еліпса однакова ea, де e – безрозмірна число від 0 до 1, яке називається ексцентриситетом. Якщо еліпс – це коло, то фактично орбіти планет досить круглі; їх ексцентриситети коливаються від 0,007 для Венери і до 0,206 для Меркурія. У земної орбіти є дві особливі точки: найближча до Сонця – це перигелій, і найбільш віддалена від сонця – афелій.

Ньютон зміг показати, що тіла, на яке діє сила тяжіння, мають єдино можливі замкнуті орбіти у вигляді кола або еліпса. А також він показав, що відкриті орбіти повинні бути параболами або
гіперболами. Ці результати можна отримати шляхом застосування законів Ньютона і закону гравітації та розв’язавши набагато більш складні диференціальні рівняння.

Другий закон Кеплера

На рисунку 2 показаний другий закон Кеплера. За невеликий проміжок часу $d t$ лінія, що з’єднує сонце S і планету P, повертається на кут $d \theta$ . На рис.2 (b) бачимо зафарбовані трикутник з висотою $r$ , довжиною основи $r d \theta$ і площею $dA = \frac{1}{2} r^2 d \theta$ . Швидкість, з якою “замітається” площа $\frac{dA}{dt}$ , називається секторною швидкістю:

(1) $\begin{equation*} \frac{dA}{dt} = \frac{1}{2}r^2\frac{d\theta}{dt} \end{equation*}$

Рисунок 2. Другий закон КеплераСуть другого закону Кеплера полягає в тому, що секторна швидкість має однакове значення в усіх точках на орбіті. Коли планета знаходиться близько до Сонця, то значення $r$ – маленьке, а $\frac{d \theta}{dt}$ – велике, а коли планета перебуває далеко від сонця, то $r$ стає великим, а $\frac{d\theta}{dt}$ – маленьким.

Щоб побачити, як з законів Ньютона випливає другий закон Кеплера, виразимо величину $\frac{dA}{dt}$ в термінах вектора швидкості $\vec{v}$ планети P. Компонента $\vec{v}$ перпендикулярна до радіальної лінії буде мати вигляд : $v_{\perp} = v\sin \phi$ . Як показано на рис. 2b переміщення вздовж напрямку $v_{\perl}$ за проміжок часу $dt$ дорівнюватиме $r d \theta$ , тому також маємо $v_{\perl} = r \frac {d \theta} {dt}$
Підставляючи це співвідношення в формулу (1), знаходимо

(2) $\begin{equation*} \frаc{dA}{dt} = \frac{1}{2} r v \sin \phi \end{equation*}$

Величина $rv \sin \phi$ є не що інше як векторний добуток $\vec{v} \times \vec{r}$ , домноживши який на $m$ отримаємо момент імпульсу планети відносно Сонця $\vec{L} = [ \vec{v} \times m \vec{r}]$ . Отже, ми маємо

(3) $\begin{equation*} \frаc{dA}{dt} = \frac{1}{2m} [\vec{v} \times m \vec{r}] = \frac{\vec{L}}{2m} \end{equation*}$

Таким чином, другий закон Кеплера говорить: секторна швидкість постійна, а з цього випливає, що кутовий момент імпульсу постійний!

Легко зрозуміти, чому момент імпульсу планети повинен бути постійним.
Знаючи, що зміна моменту імпульсу $\vec{L}$ рівна моменту $\vec{M}$ сили гравітації $\vec{F}$ , що діє на планету, маємо:

$\frac{d\vec{L}}{dt} = \vec{M} = \vec{r} \times m\vec{F}.$

В нашому випадку, $r$ – це вектор від Сонця до планети, а сила $\vec{F}$ спрямована від планети до Сонця. Таким чином, ці два вектори завжди лежать уздовж однієї і тієї ж лінії, і їх векторний добуток дорівнює нулю. Звідси $\frac{d \vec{L}}{dt}$ .
Якщо кутовий момент імпульсу зберігається, то така сила називається центральної силою.

Третій закон Кеплера

Квадрати періодів обертання планет навколо Сонця відносяться, як куби великих півосей орбіт планет.

$\frac{T^2_1}{T^2_2} = \frac{r^3_1}{r^3_2}$

З цього випливає, що період супутника або планети на круговій орбіті пропорційний степені $\frac{3}{2}$ радіуса орбіти. Ньютон зміг показати: це ж співвідношення вірно для еліптичної орбіти з заміною радіуса орбіти $r$ на велику піввісь $а$ :

$T = \frac{2 \pi a^{\frac{3}{2}}}{\sqrt{GM}}$

Зверніть увагу, що період не залежить від ексцентриситету е. Астероїд на витягнутій еліптичній орбіті з великою головною віссю $a$ матиме такий же період обертання, що і планета на круговій орбіті радіуса $a$ .
Ключова відмінність полягає в тому, що астероїд рухається з різною швидкістю в різних точках своєї еліптичної орбіти (рис. 2c), в той час як швидкість планети постійна навколо своєї кругової орбіти.