Закон Архимеда - формула, определение

Главная

›

Материалы ›

Физика ›

Механическое движение. Механика ›

Закон Архимеда

›

Выбирай среди 25000+ репетиторов из больше 100 предметов

Найти репетитора

Почему плавают корабли? Почему поднимается вверх воздушный шар? Сейчас мы начнём разбираться с этими вопросами. И снова на помощь придёт закон Архимеда.

Мы знаем, что дерево в воде не тонет. Следовательно, сила тяжести уравновешивается какой-то другой силой, действующей на кусок дерева со стороны воды вертикально вверх. Эта сила называется выталкивающей или архимедовой силой. Она действует на всякое тело, погружённое в жидкость или газ.

Выясним причину возникновения архимедовой силы. Рассмотрим цилиндр площадью поперечного сечения $S$ и высотой $h$ , погружённый в жидкость плотности $\rho$ . Основания цилиндра горизонтальны. Верхнее основание находится на глубине $h_1$ , нижнее — на глубине $h_2 = h_1 + h$ (Рисунок).

Рисунок. $F_A = F_2 - F_1$ На боковую поверхность цилиндра действуют силы давления, которые приводят лишь к сжатию цилиндра. Эти силы можно не принимать во внимание.

Найди репетитора по физики

Выбери преподавателя для подготовки к экзаменам и контрольным работам

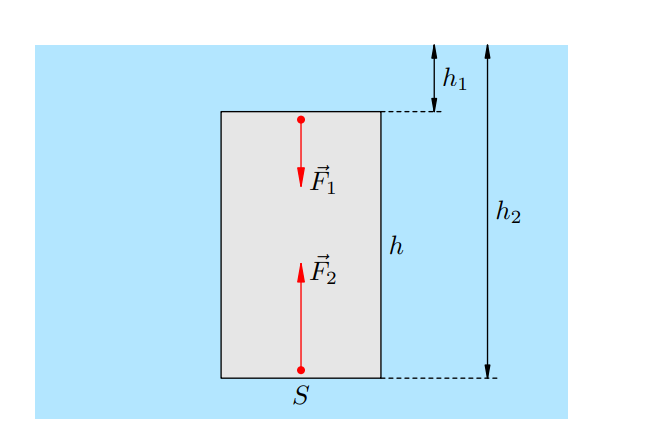
На уровне верхнего основания цилиндра давление жидкости равно $p_1 = \rho g h_1$ . На верхнее основание действует сила давления $F_1 = p_1 S = \rho g h_1 S$ , направленная вертикально вниз. На уровне нижнего основания цилиндра давление жидкости равно $p_2 = \rho g h_2$ . На нижнее основание действует сила давления $F_2 = p_2 S = \rho g h_2 S$ , направленная вертикально вверх (закон Паскаля!).

Так как $h_2$ > $h_1$ , то $F_2$ > $F_1$ , и поэтому возникает равнодействующая сил давления, направленная вверх. Это и есть архимедова сила $F_A$ . Имеем:

$F_A = F_2 - F_1 = \rho g h_2 S - \rho g h_1 S = \rho g S (h_2 - h_1) = \rho g S h .$

Но произведение $S h$ равно объёму цилиндра $V$ . Получаем окончательно:

(1) $\begin{equation*} F_A = \rho g V. \end{equation*}$

Это и есть формула для архимедовой силы. Возникает архимедова сила вследствие того, что давление жидкости на нижнее основание цилиндра больше, чем на верхнее. Формулу (1) можно интерпретировать следующим образом. Произведение $\rho V$ — это масса жидкости $m$ , объём которой равен $V : \rho V = m$ . Но тогда $\rho g V = m g = P$ , где $P$ — вес жидкости, взятой в объёме $V$ . Поэтому наряду с (1) имеем:

(2) $\begin{equation*} F_A = P. \end{equation*}$

Иными словами, архимедова сила, действующая на цилиндр, равна весу жидкости, объём которой совпадает с объёмом цилиндра. Формулы (1) и (2) справедливы и в общем случае, когда погружённое в жидкость или газ тело объёма V имеет любую форму, а не только форму цилиндра (конечно, в случае газа $\rho$ является плотностью этого газа). Поясним, почему так получается. Выделим мысленно в среде некоторый объём $V$ произвольной формы. Этот объём находится в равновесии: не тонет и не всплывает. Следовательно, сила тяжести, действующая на среду, находящуюся внутри выделенного нами объёма, уравновешена силами давления на поверхность нашего объёма со стороны остальной среды — ведь на нижние элементы поверхности приходится большее давление, чем на верхние.

Иными словами, равнодействующая сил гидростатического давления на поверхность выделенного объёма — архимедова сила — направлена вертикально вверх и равна весу среды в этом объёме. Сила тяжести, действующая на наш объём, приложена к его центру тяжести. Значит, и архимедова сила должна быть приложена к центру тяжести выделенного объёма. В противном случае сила тяжести и архимедова сила образуют пару сил, которая вызовет вращение нашего
объёма (а он находится в равновесии).

А теперь заменим выделенный объём среды твёрдым телом того же объёма $V$ и той же самой формы. Ясно, что силы давления среды на поверхность тела не изменятся, так как неизменной осталась конфигурация среды, окружающей тело. Поэтому архимедова сила попрежнему будет направлена вертикально вверх и равна весу среды, взятой в объёме $V$ . Точкой приложения архимедовой силы будет центр тяжести тела.

Закон Архимеда. На погружённое в жидкость или газ тело действует выталкивающая сила, направленная вертикально вверх и равная весу среды, объём которой равен объёму тела. Таким образом, архимедова сила всегда находится по формуле (1). Заметим, что в эту формулу не входят ни плотность тела, ни какие-либо его геометрические характеристики — при фиксированном объёме величина архимедовой силы не зависит от вещества и формы тела.

До сих пор мы рассматривали случай полного погружения тела. Чему равна архимедова сила при частичном погружении? На ту часть тела, которая находится над поверхностью жидкости, никакая выталкивающая сила не действует. Если эту часть мысленно срезать, то величина архимедовой силы не изменится. Но тогда мы получим целиком погружённое тело,
объём которого равен объёму погружённой части исходного тела.

Значит, на частично погружённое в жидкость тело действует выталкивающая сила, равная весу жидкости, объём которой равен объёму погружённой части тела. Формула (1) справедлива и в этом случае, только объём всего тела $V$ нужно заменить на объём погружённой части $V_p$ :

$F_A = \rho g V_p .$

Архимед обнаружил, что целиком погружённое в воду тело вытесняет объём воды, равный собственному объёму. Тот же факт имеет место для других жидкостей и газов. Поэтому можно сказать, что на всякое тело, погружённое в жидкость или газ, действует выталкивающая сила, равная весу вытесненной телом среды.

Плавание тел

Рассмотрим тело плотности $\rho$ и жидкость плотности $\rho_0$ . Допустим, что тело полностью погрузили в жидкость и отпустили. Сразу после отпускания на тело действуют лишь сила тяжести $m g$ и архимедова сила $F_A$ .
Если объём тела равен $V$ , то

$mg = \rho g V, F_A = \rho_0 g V .$

Имеются три возможности дальнейшего движения тела.
1. Сила тяжести больше архимедовой силы: $m g$ > $F_A$ , или $\rho$ > $\rho_0$ . В этом случае тело тонет.
2. Сила тяжести равна архимедовой силе: $m g = F_A$ , или $\rho = \rho_0$ . В этом случае тело остаётся неподвижным в состоянии безразличного равновесия.
3. Сила тяжести меньше архимедовой силы: $m g$ < $F_A$ , или $\rho$ < $\rho_0$ . В этом случае тело
всплывает, достигая поверхности жидкости. При дальнейшем всплытии начнёт уменьшаться объём погружённой части тела, а вместе с ним и архимедова сила. В какой-то момент архимедова сила сравняется с силой тяжести (положение равновесия). Тело поинерции всплывёт дальше, остановится, снова начнёт погружаться. . . Возникнут затухающие колебания, после которых тело останется плавать в положении равновесия $( m g = F_A )$ , частично погрузившись в жидкость.

Таким образом, условие плавания тела можно записать в виде неравенства: $\rho \leqslant \rho_0$ . Например, лёд ( $\rho$ = 900 кг/м³ ) будет плавать в воде ( $\rho_0$ = 1000 кг/м³), но утонет в спирте ( $\rho_0$ = 800 кг/м³ ).