Сила пружності

Як ми знаємо, в правій частині другого закону Ньютона стоїть рівнодіюча (тобто векторна сума) всіх сил, прикладених до тіла. Тепер нам належить вивчити сили взаємодії тіл в механіці. Їх три види: сила пружності, гравітаційна сила і сила тертя. Починаємо з сили пружності.

Деформація

Сили пружності виникають при деформаціях тіл. Деформація – це зміна форми і розмірів тіла. До деформацій відносяться розтяг, стиск, кручення, зрушення і вигин. Деформації бувають пружними і пластичними. Пружна деформація повністю зникає після зняття зовнішнього впливу, яке викликало деформацію. В результаті деформоване спочатку тіло відновлює свої початкові розміри і форму.

Знайди репетитора з фізики

Обери викладача для підготовки до іспитів та контрольних робіт

Шукати репетитора

Пластична деформація зберігається (можливо, частково) після зняття зовнішнього навантаження, і тіло вже не повертається до колишніх розмірів і форми. Частинки тіла (молекули або атоми) взаємодіють один з одним силами тяжіння і відштовхування, що мають електромагнітне походження (це сили, що діють між ядрами і електронами сусідніх атомів). Сили взаємодії залежать від відстаней між частинками. Якщо деформації немає, то сили тяжіння компенсуються силами відштовхування. При деформації змінюються відстані між частинками, і баланс сил взаємодії порушується.

Наприклад, при розтягуванні стержня відстані між його частинками збільшуються, і починають переважати сили тяжіння. Навпаки, при стисненні стержня відстані між частинками зменшуються, і починають переважати сили відштовхування. У будь-якому випадку виникає сила, яка направлена ​​в сторону, протилежну деформації, і яка прагне відновити первинну конфігурацію тіла.

Сила пружності – це сила, що виникає при пружній деформації тіла і спрямована в бік, протилежний зміщенню частинок тіла в процесі деформації. Сила пружності:

1. діє між сусідніми шарами деформованого тіла і прикладена до кожного шару;
2. діє з боку деформованого тіла на тіло, яке дотикаэться до нього, що викликає деформацію, і прикладена в місці контакту цих тіл перпендикулярно їх поверхням (типовий приклад – сила реакції опори).

Сили, що виникають при пластичних деформаціях, не належать до сил пружності. Ці сили залежать не від величини деформації, а від швидкості її виникнення. Вивчення таких сил виходить далеко за рамки шкільної програми. У шкільній фізиці розглядаються розтягування ниток і тросів, а також розтягування і стиснення пружин і стрижнів. У всіх цих випадках сили пружності спрямовані уздовж осей даних тіл.

Закон Гука

Деформація називається малою, якщо зміна розмірів тіла багато менше його початкових розмірів. При малих деформаціях залежність сили пружності від величини деформації виявляється лінійної. Закон Гука. Абсолютна величина сили пружності прямо пропорційна величині деформації. Зокрема, для пружини, стиснутої або розтягнутої на величину , сила пружності дається формулою:

(1)  

де – коефіцієнт жорсткості пружини.

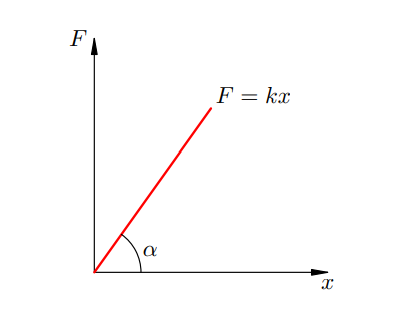
Коефіцієнт жорсткості залежить не тільки від матеріалу пружини, але також від її форми і розмірів. З формули (1) слід, що графік залежності сили пружності від (малої) деформації є прямою лінією (Дивитися малюнок):

Коефіцієнт жорсткості – це кутовий коефіцієнт в рівнянні прямої . Тому справедлива рівність:

де – кут нахилу даної прямої до осі абсцис. Це рівність зручно використовувати при експериментальному знаходженні величини .

Підкреслимо ще раз, що закон Гука про лінійну залежність сили пружності від величини деформації справедливий лише при малих деформаціях тіла. Коли деформації перестають бути малими, ця залежність перестає бути лінійною і набуває більш складний вид. Відповідно, пряма лінія на малюнку вище – це лише невеликий початкова ділянка криволинейного графіка, що описує залежність від при всіх значеннях деформації .

Модуль Юнга

В окремому випадку малих деформацій стержнів є більш детальна формула, уточнююча загальний вигляд (1) закону Гука. Саме, якщо стержень довжиною і площею поперечного перерізу розтягнути або стиснути на величину , то для сили пружності справедлива формула:

Тут – модуль Юнга матеріалу стержня. Цей коефіцієнт вже не залежить від геометричних розмірів стержня. Модулі Юнга різних речовин приведені в довідкових таблицях.