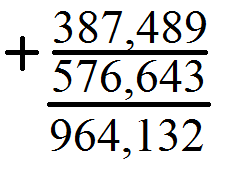Операції додавання та віднімання дробів

В попередній статті ми ознайомилися з видами дробів, і оскільки дроби – це частини цілого, то їх як і цілі числа можна віднімати і додавати.

З десятковими дробами все просто – операції додавання і віднімання проводяться аналогічним чином, як і для цілих чисел. Власне тому десяткові дроби зручні, а всі операції над ними можна провести в тому числі і на калькуляторі.  Проте, якщо калькулятора немає під рукою чи його використання заборонене умовами тесту, то десяткові дроби доведеться  додавати чи віднімати в стовпчик. Для цього головне поставити кому, яка розділяє цілу і дробову частину, одного дробу над такою ж комою  іншого дробу. Наприклад потрібно додати числа і , отримаємо

 Додавання і віднімання простих дробів є більш  поширенішою задачею в математиці і, можна сказати, що ці дії складають основу шкільної алгебри, оскільки проводяться не лише над числами, але й над буквами і виразами, що складаються з букв, тригонометричних функцій, логарифмів і т.д. (з тригонометричними функціями і логарифмами познайомимось в наступних статтях).

Найпростіше додавати дроби з однаковими знаменниками, в такому випадку потрібно лише додати чисельники, а знаменник написати спільний для двох дробів:

   

Якщо розглянути додавання на прикладі торту, що розділений на шматки, то матимемо таку ситуацію: кожен з двох тортів поділений на 8 шматків, про що свідчать знаменники дробів, і з першого торту взято 3 шматки, а з другого 7 шматків (чисельники дробів), в результаті отримаємо 10 шматків тортів, що поділені на 8 частин:

Аналогічно для віднімання – чисельники віднімаємо, а знаменник пишемо спільний для двох дробів:

   

І в загальному вигляді:

   

де , i – будь-які цілі числа.

Якщо ж знаменники дробів не однакові, то на практиці це означає, що наші торти поділені на різну кількість частин, а тому шматки мають різний розмір і як їх додавати чи віднімати незрозуміло. Відповідно завдання полягає  в тому, щоб  зробити шматки тортів однаковими за розміром, тобто знайти спільний знаменник, а в цьому нам допоможе основна властивість дробів, яку ми згадали в попередній статті “Види дробів“.

Спочатку розберемось, що значить знайти найменше спільне кратне (НСК) для двох цілих чисел і (два будь-яких цілих числа) – це означає відшукати таке найменше число, яке б ділилося як на , так і на без остачі. Наприклад, потрібно знайти НСК для і , оскільки числа невеликі, то можна без проблем сказати, що найменшим числом, яке б ділилося і на , і на є число . Проте якщо числа будуть більшими, то вже не так легко буде знайти НСК. В такому випадку на допомогу приходять правила з пошуку найменшого спільного кратного двох чисел:

• • 1. Розкласти кожне з чисел на прості множники (числа, що діляться лише на себе і на одиницю: 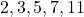і т.д.),
    2. Беремо будь-яке з двох розкладених чисел і домножаємо його, на ті прості множники, яких бракує в іншому – це і буде найменше спільне кратне.

Приклад 1.

Знайти НСК і .

Розв’язок.

Спершу розкладаємо на множники обидва числа:

Беремо число і порівнюємо його розклад з розкладом числа . Бачимо, що в розкладі 36 дві двійки і дві трійки, тобто не вистачає ще однієї двійки і однієї трійки, щоб могло повноцінно увійти в розклад , тому домножаємо на та  і отримуємо НСК цих двох чисел
Так само ми могли взяти розклад і порівняти його з розкладом , в такому випадку можна побачити, що в розклад не входить число , таким чином, щоб знайти НСК і треба домножити на , після перемноження отримаємо .

 Приклад 2.

Знайти НСК і .

Розв’язок.

В розкладі не вистачає двох двійок, якщо його порівнювати з розкладом , отже, НСК буде

Якщо потрібно знайти НСК трьох і більше чисел, то потрібно розкласти на прості множники кожне із чисел. Потім обрати перше число, порівняти його розклад з розкладом другого числа  і домножити на бракуючі множники, розклад утвореного числа  порівняти з розкладом третього числа і знову домножити його на бракуючі прості множники і т.д.

Знаючи як шукати найменше спільне кратне, можемо перейти до додавання двох дроби з різними знаменниками. Почнемо з прикладу:

   

Для цього потрібно знайти спільний знаменник, що рівноцінно знаходженню найменшого спільного кратного для чисел, що є знаменниками двох дробів. Застосовуючи правила для знаходження НСК, маємо спільний знаменник . В такому випадку чисельник першого дробу не потрібно домножити на , а чисельник другого дробу на , маємо

   

Таким чином, щоб додати або ж відняти два дроби з різними знаменниками потрібно:

1. Знайти спільний знаменник двох дробів, використовуючи правила для знаходження найменшого спільного кратного.
2. Домножити кожен із чисельників дробу на число, яке знаходимо з допомогою ділення знайденого спільного знаменника на чисельник обраного дробу.
3. Виконати операцію додавання чи віднімання в чисельнику дробу зі спільним знаменником.