Коливальний рух, амплітуда, частота коливань, види маятників.
1. Коливальний рух
Коливальний рух є одним з найпоширеніших у природі видів руху, і всі ми його неодноразово спостерігали. Коливаються гойдалка, гілки й листя дерев на вітрі, струни музичних інструментів і голосові зв’язки людини, коли видають звуки.
Коливальний рух здійснює і тіло, підвішене на пружині. Якщо тіло штовхнути у вертикальному напрямку, то можна побачити, що воно рухається вниз-вгору, тобто здійснює коливальний рух.
Якщо ми подивимося на рух вантажу на нитці, то помітимо, що він буде рухатися від одного крайнього положення до іншого, проходячи через середню точку й повторюючи свій рух через певний проміжок часу. Такий рух вантажу також являє приклад механічних коливань.
•Коливаннями називаються фізичні процеси, що точно або приблизно повторюються через однакові інтервали часу.
Залежно від фізичної природи розрізняють механічні й електромагнітні коливання.
•Механічними коливаннями називаються такі рухи тіл, за яких через рівні інтервали часу координати тіла, що рухається, його швидкість і прискорення приймають вихідні значення.
2. Амплітуда, період і частота коливань
Підвісимо на дві нитки однакової довжини однакові вантажі. Відхилимо вантажі обох маятників на різні відстані. Ми помітимо, що обидва маятники будуть коливатися з різними розмахами, тобто їхні крайні положення перебувають на різних відстанях від положення рівноваги.

«Розмах» коливань, тобто найбільше відхилення коливального тіла від положення рівноваги, називається амплітудою коливання.
• Амплітуда коливань — це максимальна відстань, на яку відхиляється тіло, що коливається, від свого положення рівноваги.
Амплітуду коливань позначають символом А й вимірюють у метрах (м).
•Час, за який тіло робить одне повне коливання, називається періодом коливання – T.
•Частота коливань ν— це число коливань в одиницю часу.
За одиницю частоти приймають частоту коливань, за якої за 1 с здійснюється одне повне коливання. Ця одиниця називається герцом (Гц).
Період і частота коливань зв’язані між собою формулою T = 1/ν.
3. Математичний маятник
Розглянемо коливання вантажу, підвішеного на нитці. Якщо взяти нитку довжиною, набагато більшою від розміру вантажу, і масою нитки, набагато меншою від маси вантажу, то ми одержимо модель «математичного маятника».
•Математичним маятником називається ідеалізована коливальна система без тертя, що складається з невагомої й нерозтяжної нитки, на якій підвішена матеріальна точка.
Відводячи маятник на більшу або меншу відстань, ми можемо змінювати амплітуду його коливань. Вимірюючи період коливань при різних амплітудах, ми дійдемо висновку, що якщо амплітуда коливань набагато менше довжини нитки, то період коливань практично не залежить від їхньої амплітуди.
Вимірюючи період коливань маятника при різних масах вантажу, ми виявимо, що період коливань математичного маятника не залежить від маси вантажу.
Вимірюючи період коливань маятника при різних довжинах нитки, ми виявимо, що зі збільшенням довжини нитки період коливань збільшується.
При збільшенні довжини нитки в 4 рази період коливань збільшується у 2 рази, а при збільшенні довжини нитки в 9 разів період коливань збільшується в 3 рази.
Це дозволяє припустити, що період коливань математичного маятника пропорційний кореню квадратному з довжини нитки: ![]()
4. Пружинний маятник
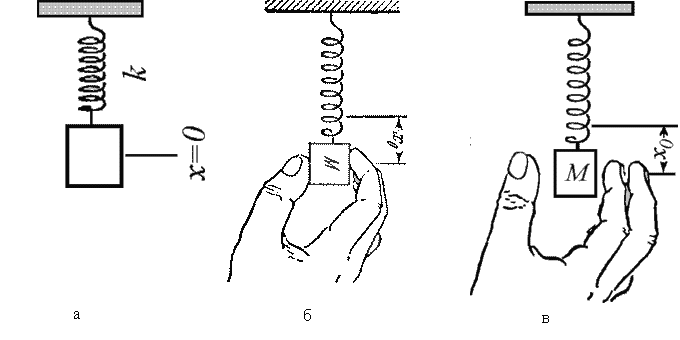
Друга коливальна система, яка називається пружинним маятником, являє собою підвішений на легкій пружині вантаж, що здійснює коливання уздовж прямої.
Вимірюючи період коливань пружинного маятника при різних амплітудах, ми помітимо, що, так само, як і для математичного маятника, період коливань практично не залежить від їхньої амплітуди. Це головна загальна властивість пружинного й математичного маятників.
Вимірюючи період коливань маятника при різних масах вантажу, виявляємо, що чим більша маса вантажу, тим більше період коливань. При збільшенні маси в 4 рази період коливань збільшується в 2 рази, а при збільшенні маси в 9 разів період коливань збільшується в 3 рази. Це дозволяє припустити, що період коливань пружинного маятника пропорційний кореню квадратному з масивантажу.
Крім того, період коливань пружинного маятника залежить також від властивостей пружини: чим вона «м’якше», тобто чим більше видовження пружини під вагою того самого вантажу, тим більше період коливань.
Перевірте себе!
- Наведіть приклади коливальних рухів.
- Як ви розумієте твердження про те, що коливальний рух періодичний?
- Наведіть приклади фізичного, нитяного й пружинного маятників.
- Де використовують математичний маятник? Наведіть дватри приклади.
- Де використовують пружинний маятник? Наведіть два–три приклади.
