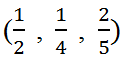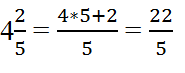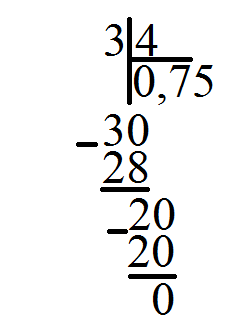Види дробів

   Дріб в математиці введений для зображення частини цілого числа. Наприклад, одна друга або половина, одна четверта або четвертина,  дві п’ятих і т.д. Всі дроби можна розділити на три види:

1.Простий або звичайний дріб

Дріб, що прийнято записувати у формі  двох цілих чисел, які відділяються горизонтальною

або скошеною ( 1/2, 1/4, 2/5)  лінією називається простим. Число, що стоїть внизу або справа (в залежності від форми запису) в простому дробі, називається знаменником, і він показую на скільки рівних частинок потрібно розділити ціле, а число вгорі або зліва – чисельник,  і він показую скільки  цих рівних частинок цілого потрібно взяти.  Що це означає на практиці, розглянемо на прикладі дробу  . Для цього візьмемо піцу і виділимо на ній цей дріб. Знаменник, тобто число 8, буде показувати на скільки шматків потрібно розрізати піцу, а чисельник, тобто число 5, буде показувати скільки шматків із цих восьми власне треба взяти.

1. Кількість частинок, на які ділиться піца 8. 

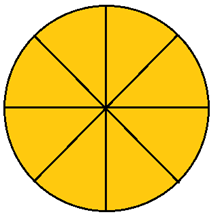
2. Кількість частинок, що ми беремо – 5.

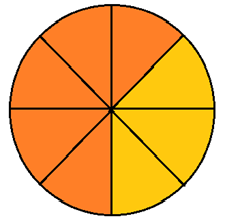
Основна властивість простого дробу.

Якщо чисельник і знаменний будь – якого дробу помножити чи поділити на одне і теж саме число, то значення дробу не зміниться:

   

Тобто, таким чином можна отримати безкінечну кількість записів одного і того ж самого дробу.

Питання в тому як ця властивість дробу використовується на практиці. Наприклад, ми маємо дріб

   

розділимо чисельник і знаменник цього дробу на п’ять і отримаємо дріб

   

а якщо знаменник і чисельник знову поділити  на 5, то взагалі отримаємо дріб:

   

Зрозуміло, що працювати з останнім дробом набагато зручніше і легше, ніж з початковим, хоча величини обох дробів однакові. Процедура ділення чисельника і знаменника на одне і теж саме число, описана на прикладі вище, називається скороченням дробу і для простоти обчислень її, за можливості, потрібно проводити завжди.
Так само можна скорочувати дріб на вирази:

   

 

   

І в старших класах, крім двох чисел,  потрібно вміти скорочувати саме вирази. Проте  багато старшокласників, взявши на озброєння процедуру скорочення, починають застосовувати її там, де це неприпустимо. Наприклад, дріб виду

   

не можна скоротити, оскільки не ділиться на жодне число, крім всього виразу в цілому . Але старшокласника це може не зупинити, і в знаменнику та чисельнику буде скорочений, і дріб перетвориться на  

   

що для вчителя буде рівноцінно невмінню працювати з дробами взагалі.

Правильний і неправильний прості дроби.

Дріб, в якому чисельник має значення менше за знаменник, називається правильним. Наприклад,

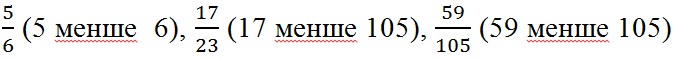
і т.д. Якщо ж значення чисельника  перевищує значення  знаменника, то такий дріб називається неправильним. Наприклад,

і т.д. Повертаючись до піци, неправильний дріб 9/4 означає, що наша піца була поділена на 4 шматки і таких шматків було взято 9, тобто більше, ніж складає одна піца, а якщо точніше, то 9 таких шматків складатимуть 2 цілих піци і ще одну четвертинку. Це означає, що в неправильному дробі можна виділити цілу частину (цілі піци).

 

 

 3.Дріб 9/4.

2.Змішаний дріб.

Дріб, що записується як ціле число і поряд простий правильний дріб

називається змішаним і його можна отримати, виділивши кількість цілих частин в неправильному простому дробі. Даний вид запису дробів рідко використовується, але такий запис може зустрітися в задачі, тому надалі покажемо як переходити від змішаного дробу до простого неправильного дробу. Для цього візьмемо змішаний дріб

і нашу піцу. Бачимо, що знаменник дробу дорівнює 5, а це означає, що кожну із 4 цілих піц потрібно розрізати на п’ять шматків, в результаті ми отримаємо 20 шматків. Після цього потрібно до цих 20 шматків додати ще ті два шматки, що стояли в чисельнику простого дробу – отримаємо 22 шматки, тобто неправильний простий дріб   . В математичному записі це буде виглядати так

 

3.Десятковий дріб.

Дроби записані у вигляді 0,235;   0,32;    5,6 і т.д. називаються десятковими. При чому говорять, що до коми вказана ціла частина, а після коми дробова. Важливо вміти читати таку форму запису, для того, щоб легко переходити від десяткової форми запису до простого дробу. Отже, спочатку проговорюється число перед комою і додається слово «цілих», а потім проговорюється число після коми і в залежності від кількості знаків/цифр після коми додається слово, що характеризую на скільки частин розбивається ціле: десятих, сотих, тисячних, десятитисячних і т.д.. Наприклад, запис виду 0,2 читається як «нуль цілих дві десятих»,  запис 4,32 – «чотири цілих тридцять дві сотих» і т.д.

Перетворення десяткового дробу в простий і навпаки.

Для того, щоб перейти від десяткового до простого дробу потрібно записати  десятковий дріб так як він читається, але з допомогою чисельника і знаменника, а потім, за можливості, провести процедуру скорочення. Наприклад, і після скорочення на 2 отримаємо
і після скорочення на 25 отримаємо Число після переводу в простий дріб скоротити не можна, тому це остаточна форма запису.

Часто доводиться переводити простий дріб в десятковий, зокрема для запису відповідей в тестах. Що робити, якщо, розв’язавши завдання, отримали результат у вигляді простого дробу

   

потрібно, як вчили в початковій школі, поділити в стовпчик одне число на інше .

 

Як бачимо з результатів ділення, отримаємо

   

Якщо спробувати, наприклад, дріб перевести в десятковий, тобто виконати процедуру ділення в стовпчик, то отримаємо число  і так трійки до безкінечності. Тому можна зробити висновок, що не будь-який десятковий дріб переводиться звичайний (простий) дріб.

Якою ж формою запису дробу користуватися найкраще? Звичайно ж, це залежить від ситуації. Наприклад, якщо у вас є завдання, де дроби знаходяться в усіх трьох видах, в такому випадку надійніше перевести всі ці дроби  в звичайні і потім проводити обчислення. Якщо в завданні пропонується порахувати  десяткові дроби, то звичайно ж переходити до простих дробів не потрібно. Тобто ми обираємо той спосіб розв’язку, що є найбільш зручнішим.